题目内容

函数y=
log
1
2
(x-3)
的定义域是（　　）
A、（-∞，4）
B、（-∞，4]
C、（3，4]
D、（3，4）
考点：对数函数的定义域
专题：函数的性质及应用
分析：函数y=
log
1
2
(x-3)
的定义域满足
log
1
2
(x-3)≥0
x-3＞0
，由此能求出函数y=
log
1
2
(x-3)
的定义域．
解答： 解：函数y=
log
1
2
(x-3)
的定义域满足：
log
1
2
(x-3)≥0
x-3＞0
，
解得3＜x≤4，
∴函数y=
log
1
2
(x-3)
的定义域为（3，4]．
故选：C．
点评：本题考查函数的定义域的求法，是基础题，解题时要注意对数函数的性质的合理运用．
练习册系列答案
相关题目
设定义域为（0，+∞）的单调函数f（x），对任意的x∈（0，+∞），都有f[f（x）-log2x]=3，若函数f（x）与函数g（x）的图象关于直线y=x对称，则函数g（x）=
 
．
函数f（x）=2sin（x-
π
3
），x∈[-π，0]的单调递增区间是（　　）
A、[-π，-
5π
6
]
B、[-
5π
6
，-
π
6
]
C、[-
π
3
，0]
D、[-
π
6
，0]
某设备的使用年限与所支出的维修费用的统计数据如下表：
使用年限x（单位：年）23456
维修费用y（单位：万元）1.54.55.56.57.0
根据上表可得回归直线方程为：
∧
y
=1.3x+
∧
a
，据此模型预测，若使用年限为8年，估计维修费用约为（　　）
A、10.2万元
B、10.6万元
C、11.2万元
D、11.6万元
函数f（x）=|sinx|+
1
2
sinx（0≤x≤2π）与函数g（x）=a（a是常数）有两个不同的交点，则a的取值范围是（　　）
A、（0，
3
2
）
B、（-
1
2
，0）∪（0，
3
2
）
C、（0，
1
2
）
D、（
1
2
，
3
2
）
对于函数f（x）=cos（
π
2
-2x），下列选项中正确的是（　　）
A、f（x）在(
π
4
， 
π
2
)上是递增的
B、f（x）的图象关于原点对称
C、f（x）的最小正周期为2π
D、f（x）的最大值为2
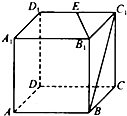如图，在正方体ABCD-A1B1C1D1中，棱长AB=2，点E是棱C1D1的中点，则异面直线B1E和BC1所成角的余弦值为（　　）
A、
15
5
B、
10
5
C、
15
10
D、
10
10
已知直线的倾斜角为135°，在x轴上的截距为2，则此直线方程为（　　）
A、y=x+2．
B、y=x-2
C、y=-x+2
D、y=-x-2
函数f（x）=
3
sinx+cosx的最大值是（　　）
A、1B、2C、3D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网