题目内容
4.若向量$\overrightarrow{a}$=(-1,x)与$\overrightarrow{b}$=(-x,3)共线且方向相反,则x=-$\sqrt{3}$.分析 利用向量共线定理及其方向相反即可得出.
解答 解:向量$\overrightarrow{a}$=(-1,x)与$\overrightarrow{b}$=(-x,3)共线,
∴-x2=-3,
解得x=±$\sqrt{3}$,
∵向量$\overrightarrow{a}$=(-1,x)与$\overrightarrow{b}$=(-x,3)共线且方向相反,
∴x=-$\sqrt{3}$,
故答案为:-$\sqrt{3}$.
点评 熟练掌握向量共线定理及其方向相反是解题的关键.

练习册系列答案
相关题目
14.已知非零正实数x1,x2,x3依次构成公差不为零的等差数列,设函数f(x)=xα,α∈{-1,$\frac{1}{2}$,2,3},并记M={-1,$\frac{1}{2}$,2,3}.下列说法正确的是( )
| A. | 存在α∈M,使得f(x1),f(x2),f(x3)依次成等差数列 | |
| B. | 存在α∈M,使得f(x1),f(x2),f(x3)依次成等比数列 | |
| C. | 当α=2时,存在正数λ,使得f(x1),f(x2),f(x3)-λ依次成等差数列 | |
| D. | 任意α∈M,都存在正数λ>1,使得λf(x1),f(x2),f(x3)依次成等比数列 |
19.若z2+z+1=0,则z2002+z2003+z2005+z2006等于( )
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i | D. | -$\frac{1}{2}$±$\frac{\sqrt{3}}{2}$i |
2.直线a、b是异面直线,α、β是平面,若a?α,b?β,α∩β=c,则下列说法正确的是( )
| A. | c至少与a、b中的一条相交 | B. | c至多与a、b中的一条相交 | ||
| C. | c与a、b都相交 | D. | c与a、b都不相交 |
3.下列命题为真命题的是( )
| A. | 已知x,y∈R,则$\left\{\begin{array}{l}{x>1}\\{y>2}\end{array}\right.$是$\left\{\begin{array}{l}{x+y>3}\\{xy>2}\end{array}\right.$的充要条件 | |
| B. | 当0<x≤2时,函数y=x-$\frac{1}{x}$无最大值 | |
| C. | ?a,b∈R,$\frac{a+b}{2}≥\sqrt{ab}$ | |
| D. | ?x∈R,sinx+cosx=$\frac{7}{5}$ |
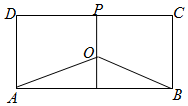 节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形ABCD的两个顶点A、B及CD的中点P处,AB=30km,BC=15km,为了处理三家工厂的污水,现要在该矩形区域上(含边界),且与A、B等距离的一点O处,建造一个污水处理厂,并铺设三条排污管道AO、BO、PO.设∠BAO=x(弧度),排污管道的总长度为ykm.
节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形ABCD的两个顶点A、B及CD的中点P处,AB=30km,BC=15km,为了处理三家工厂的污水,现要在该矩形区域上(含边界),且与A、B等距离的一点O处,建造一个污水处理厂,并铺设三条排污管道AO、BO、PO.设∠BAO=x(弧度),排污管道的总长度为ykm.