题目内容
设A=
，B=
，若AB=BA，求k的值．
|
|
考点：矩阵与向量乘法的意义
专题：矩阵和变换
分析：由已知中A=
，B=
，分别求出AB和BA，结合AB=BA，可得k的值．
|
|
解答：
解：∵设A=
，B=
，
∴AB=
，BA=
，
又∵AB=BA，
∴k=3．
|
|
∴AB=
|
|
又∵AB=BA，
∴k=3．
点评：本题考查的知识点是矩阵乘法，矩阵相等，其中分别求出AB，BA是解答的关键．
练习册系列答案
相关题目
如图是正四面体的平面展开图，G、H、M、N分别为DE、BE、EF、EC的中点，在这个正四面体中，
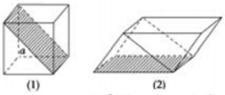如图（1）所示，已知正方体面对角线长为a，沿阴影面将它切割成两块，拼成如图（2）所示的几何体，那么此几何体的表面积为（ ）A、（1+2
| ||
B、（2+
| ||
C、（3+2
| ||
D、（4+
|
