Question

设O是坐标原点，定点A（1，0），M是直线l：x=2上的点，过点A作OM的垂线，垂足为R，且所作的垂线与以OM为直径的圆C交于P、Q两点．
（1）若PQ=

6

，求圆C的方程；
（2）若M是直线l上的动点，求证：点P在定圆上，并求该定圆的方程．

Answer 1

考点：圆的标准方程,直线与圆相交的性质

专题：直线与圆

分析：（1）设圆C与x轴相交与点N，利用射影定理得：OQ²=OR•OM，QR²=OR•RM=(

6

2

)2=

3

2

，由△OAR∽△OMN，可得

OA

OM

=

OR

ON

，可求得OQ=

2

，OR=

OQ2-RQ2

=

2

2

，
OM=2

2

，进一步可求得M（2，2），于是可求圆C的方程方程为：（x-1）²+（y-1）²=2；
（2）由（1）OP²=OQ²=OR•OM=OF•OA=2，可求得OP=

2

，于是可知P在以O为圆心，

2

为半径的圆上，继而可得定圆方程为：x²+y²=2．

解答： 解：∵OM为圆C的直径，PQ⊥OM，且PQ=

6

，设圆C与x轴相交与点N，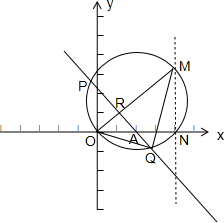
由射影定理得：OQ²=OR•OM，QR²=OR•RM=(

6

2

)2=

3

2

，△OAR∽△OMN，
∴

OA

OM

=

OR

ON

，即
OA•ON=OR•OM=2，∴OQ=

2

，OR=

OQ2-RQ2

=

2

2

，
∴OM=2

2

，MN=

OM2-ON2

=2，
∴M（2，2），∴圆C的方程为：（x-1）²+（y-1）²=2；
（2）由（1）OP2=OQ2=OR•OM=OF•OA=2，∴OP=

2

，
∴P在以O为圆心，

2

为半径的圆上，
∴定圆方程为：x²+y²=2．

点评：本题考查圆的方程及其应用，考查射影定理及相似三角形的应用，求得圆C的方程是难点，也是关键，考查分析．运算能力，属于难题．