题目内容
2.已知直角三角形的三边长都是整数且其面积与周长在数值上相等,那么这样的直角三角形有( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 设两条直角边为a,b,斜边为c,从而可得a2+b2=c2,$\frac{1}{2}$ab=a+b+c,从而化简可得(a-4)(b-4)=8,从而解得.
解答 解:设两条直角边为a,b,斜边为c,
则面积S=$\frac{1}{2}$ab,周长l=a+b+c,a2+b2=c2;
又∵2ab=(a+b)2-(a2+b2)=(a+b)2-c2=(a+b+c)(a+b-c)
∴$\frac{1}{2}$ab=$\frac{1}{4}$(a+b+c)(a+b-c),
∵$\frac{1}{2}$ab=a+b+c,
∴(a+b+c)(a+b-c)/4=a+b+c
∴$\frac{1}{4}$(a+b-c)=1,
∴a+b-c=4,
∴a2+b2=c2=(a+b-4)2=a2+b2+16-8a-8b+2ab
∴16-8a-8b+2ab=0,
即ab-4a-4b+8=0,
即(a-4)(b-4)=8,
又∵边长为整数,
∴a-4=1,2,4,8,-1,-2,-4,-8
∴a=5,6,8,12,0,2,0,-4
又∵a>0,
∴a=5,6,8,12,2,
∴b=12,8,6,5,0,
又∵a,b,c都是整数,
∴有两种直角三角形,
分别是6,8,10和5,12,13;
故边长为整数,且面积等于周长的直角三角形一共有2个.
点评 本题考查了直角三角形的性质与完全平方式的应用,属于中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
14.△ABC的内角A,B,C的对边分别为a,b,c,满足$\frac{a-b+c}{b}≤\frac{c}{a+b-c}$,则角A的范围是( )
| A. | $({0,\frac{π}{6}}]$ | B. | $({0,\frac{π}{3}}]$ | C. | $[{\frac{π}{6},π})$ | D. | $[{\frac{π}{3},π})$ |
12.表是某市从3月份中随机抽取的10天空气质量指数(AQI)和“PM2.5”(直径小于等于2.5微米的颗粒物)24小时平均浓度的数据,空气质量指数(AQI)小于100表示空气质量优良.
(1)根据表数据,估计该市当月某日空气质量优良的概率;
(2)在表数据中、在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件M为“抽取的两个日期中,当天‘PM2.5’的24小时平均浓度小于75ug/m3”,求事件M发生的概率.
| 日期编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 空气质量指数(AQI) | 179 | 40 | 98 | 124 | 29 | 133 | 241 | 424 | 95 | 89 |
| PM2.5日均浓度(ug/m3) | 135 | 5 | 80 | 94 | 80 | 100 | 190 | 387 | 70 | 66 |
(2)在表数据中、在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件M为“抽取的两个日期中,当天‘PM2.5’的24小时平均浓度小于75ug/m3”,求事件M发生的概率.
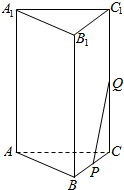 如图,在正三棱柱ABC-A1B1C1中,已知它的底面边长为10,高为20.
如图,在正三棱柱ABC-A1B1C1中,已知它的底面边长为10,高为20. 过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C两点.若PA=6,AC=4,BC=9,求AB的值.
过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C两点.若PA=6,AC=4,BC=9,求AB的值.