题目内容
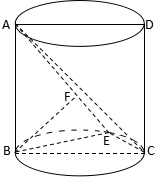 如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,BF⊥AE,F是垂足.
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,BF⊥AE,F是垂足.(1)求证:BF⊥AC;
(2)若CE=1,∠CBE=30°,求三棱锥F-BCE的体积.
考点:旋转体(圆柱、圆锥、圆台)
专题:计算题,空间位置关系与距离
分析:(1)欲证BF⊥AC,先证BF⊥平面AEC,根据线面垂直的判定定理可知只需证CE⊥BF,BF⊥AE且CE∩AE=E,即可证得线面垂直;
(2)VF-BCE=VC-BEF=
•S△BEF•CE=
•
•EF•BF•CE,即可求出三棱锥F-BCE的体积.
(2)VF-BCE=VC-BEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
解答:
 (1)证明:∵AB⊥平面BEC,CE?平面BEC,∴AB⊥CE
(1)证明:∵AB⊥平面BEC,CE?平面BEC,∴AB⊥CE
∵BC为圆的直径,∴BE⊥CE.
∵BE?平面ABE,AB?平面ABE,BE∩AB=B
∴CE⊥平面ABE,
∵BF?平面ABE,
∴CE⊥BF,
又BF⊥AE且CE∩AE=E,
∴BF⊥平面AEC,
∵AC?平面AEC,
∴BF⊥AC…(6分)
(2)解:在Rt△BEC中,∵CE=1,∠CBE=30°∴BE=
,BC=2
又∵ABCD为正方形,∴AB=2,∴AE=
,
∴BF•AE=AB•BE,
∴BF=
,∴EF=
∴VF-BCE=VC-BEF=
•S△BEF•CE=
•
•EF•BF•CE
=
•
•
•
•1=
…(12分)
 (1)证明:∵AB⊥平面BEC,CE?平面BEC,∴AB⊥CE
(1)证明:∵AB⊥平面BEC,CE?平面BEC,∴AB⊥CE∵BC为圆的直径,∴BE⊥CE.
∵BE?平面ABE,AB?平面ABE,BE∩AB=B
∴CE⊥平面ABE,
∵BF?平面ABE,
∴CE⊥BF,
又BF⊥AE且CE∩AE=E,
∴BF⊥平面AEC,
∵AC?平面AEC,
∴BF⊥AC…(6分)
(2)解:在Rt△BEC中,∵CE=1,∠CBE=30°∴BE=
| 3 |
又∵ABCD为正方形,∴AB=2,∴AE=
| 7 |
∴BF•AE=AB•BE,
∴BF=
2
| ||
|
| 3 | ||
|
∴VF-BCE=VC-BEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 | ||
|
2
| ||
|
| ||
| 7 |
点评:本小题主要考查空间线面关系、圆柱性质、空间想象能力和逻辑推理能力,考查三棱锥F-BCE的体积的计算,属于中档题.

练习册系列答案
相关题目
已知x,y满足
,则
的最小值为( )
|
| (x-2)2+(y+1)2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 某物流公司运费计算框图如图所示,其中d为按运送里程给运费打的折扣,n为运送物品的件数.现有顾客办理A、B两件物品递送,其中A物品运送单价为p1=0.02元/千克•千米,重量为w1=5千克,运送里程为s1=250千米;B物品运送单价为p2=0.03元/千克•千米,重量为w2=6千克,运送里程为s2=500千米.则按运费计算框图算出该顾客应付运费sum=( )
某物流公司运费计算框图如图所示,其中d为按运送里程给运费打的折扣,n为运送物品的件数.现有顾客办理A、B两件物品递送,其中A物品运送单价为p1=0.02元/千克•千米,重量为w1=5千克,运送里程为s1=250千米;B物品运送单价为p2=0.03元/千克•千米,重量为w2=6千克,运送里程为s2=500千米.则按运费计算框图算出该顾客应付运费sum=( )