题目内容
证明不等式1+
+
+…+
<
(n∈N*)
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (n+1)2 |
| 2n+1 |
| n+1 |
考点:数学归纳法
专题:证明题,推理和证明
分析:利用数学归纳法证明(1)当n=1时,验证不等式成立;(2)假设n=k(k≥1)时,不等式成立,然后证明当n=k+1时,不等式也成立.即可得出结论.
解答:
证明:(1)当n=1时,不等式左端=1+
=
,右端=
,所以不等式成立;
(2)假设n=k(k≥1)时,不等式成立,即1+
+
+…+
<
,
则n=k+1时,不等式左端=1+
+
+…+
+
<
+
,
∵
+
-
=
<0,
∴
+
<
,
∴1+
+
+…+
+
<
,
∴当n=k+1时,不等式也成立.
综合(1)、(2)得:当n∈N*时,都有1+
+
+…+
<
.
| 1 |
| 22 |
| 5 |
| 4 |
| 3 |
| 2 |
(2)假设n=k(k≥1)时,不等式成立,即1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (k+1)2 |
| 2k+1 |
| k+1 |
则n=k+1时,不等式左端=1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (k+1)2 |
| 1 |
| (k+2)2 |
| 2k+1 |
| k+1 |
| 1 |
| (k+2)2 |
∵
| 2k+1 |
| k+1 |
| 1 |
| (k+2)2 |
| 2k+3 |
| k+2 |
| -1 |
| (k+1)(k+2)2 |
∴
| 2k+1 |
| k+1 |
| 1 |
| (k+2)2 |
| 2k+3 |
| k+2 |
∴1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (k+1)2 |
| 1 |
| (k+2)2 |
| 2k+3 |
| k+2 |
∴当n=k+1时,不等式也成立.
综合(1)、(2)得:当n∈N*时,都有1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (n+1)2 |
| 2n+1 |
| n+1 |
点评:本题考查数学归纳法证明不等式的应用,考查逻辑推理能力,计算能力以及转化思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若x,y满足约束条件
则3x+2y 的取值范围( )
|
A、[
| ||
B、[
| ||
C、[
| ||
D、[
|
在△ABC中,三内角A,B,C的对边分别为a,b,c,面积为S,若S+a2=(b+c)2,则cosA等于( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|

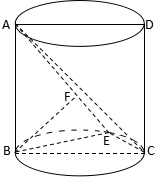 如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,BF⊥AE,F是垂足.
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,BF⊥AE,F是垂足.