题目内容
已知α,β均为锐角,且cos(α+β)=
,则tanα的最大值是 .
| sinα |
| sinβ |
考点:两角和与差的正弦函数
专题:函数的性质及应用,三角函数的求值
分析:直接对三角函数关系式中的角进行恒等变换,再利用弦化切建立一元二次不等式,最后求出结果.
解答:
解:知α,β均为锐角,且cos(α+β)=
,
则cos(α+β)sinβ=sinα=sin[(α+β)-β],
化简为:cos(α+β)sinβ=sin(α+β)cosβ-cos(α+β)sinβ,
转化为:tan(α+β)=2tanβ,
即
=2tanβ,
则:2tanαtan2β-tanβ+tanα=0,
所以:△≥0,
即:1-8tan2α≥0,
解得:-
≤tanα≤
.
由于:α为锐角,
所以:0<tanα≤
,
则tanα的最大值为
.
故答案为:
| sinα |
| sinβ |
则cos(α+β)sinβ=sinα=sin[(α+β)-β],
化简为:cos(α+β)sinβ=sin(α+β)cosβ-cos(α+β)sinβ,
转化为:tan(α+β)=2tanβ,
即
| tanα+tanβ |
| 1-tanαtanβ |
则:2tanαtan2β-tanβ+tanα=0,
所以:△≥0,
即:1-8tan2α≥0,
解得:-
| ||
| 4 |
| ||
| 4 |
由于:α为锐角,
所以:0<tanα≤
| ||
| 4 |
则tanα的最大值为
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题考查的知识要点:三角函数关系式中角的恒等变换,弦化切在做题中得应用,一元二次不等式有解得情况讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设不等式组
表示的平面区域为D,则区域D的面积为( )
|
| A、10 | B、15 | C、20 | D、25 |
双曲线
-
=1的右焦点到抛物线y2=4x的准线的距离为( )
| x2 |
| 4 |
| y2 |
| 12 |
| A、5 | B、4 | C、3 | D、2 |
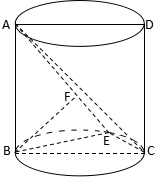 如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,BF⊥AE,F是垂足.
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,BF⊥AE,F是垂足.