题目内容
已知等边△ABC的边长为3,M是△ABC的外接圆上的动点,则
•
的最大值为 .
| AB |
| AM |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:画出图形,
•
=|
||
|cos∠BAM=3|
|cos∠BAM,设OM是外接圆⊙O的半径,则 当
∥
且同向时,则
•
取得最大值.
| AB |
| AM |
| AB |
| AM |
| AM |
| OM |
| AB |
| AB |
| AM |
解答:
解:如图,
•
=|
||
|cos∠BAM=3|
|cos∠BAM,设OM是外接圆⊙O的半径为3×
×
=
,
则 当
∥
且同向时,则
•
取得最大值.
所以3|
|cos∠BAM=3(
+OM)=
;
故答案为:
.
| AB |
| AM |
| AB |
| AM |
| AM |
| ||
| 2 |
| 2 |
| 3 |
| 3 |
则 当
| OM |
| AB |
| AB |
| AM |
所以3|
| AM |
| AB |
| 2 |

9+6
| ||
| 2 |
故答案为:
9+6
| ||
| 2 |
点评:本题考查了向量的数量积运算、向量的投影,考查了推理能力和计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某仓库失窃,四个保管员因涉嫌而被传讯,四人供述如下
甲:我们四人都没有作案;
乙:我们四人有人作案;
丙:乙和丁至少有一个人没作案;
丁:我没有作案.
如果四人中有两个人说的是真话,有两人说的是假话,则以下断定成立的是( )
甲:我们四人都没有作案;
乙:我们四人有人作案;
丙:乙和丁至少有一个人没作案;
丁:我没有作案.
如果四人中有两个人说的是真话,有两人说的是假话,则以下断定成立的是( )
| A、说真话的是甲和丁 |
| B、说真话的是乙和丙 |
| C、说真话的是甲和丙 |
| D、说真话的是乙和丁 |
设a,b>0,a≠b,lna-lnb=a-b,给出下列结论:
①0<ab<1;②0<a+b<2;③a+b-ab>1.
其中所有正确结论的序号是( )
①0<ab<1;②0<a+b<2;③a+b-ab>1.
其中所有正确结论的序号是( )
| A、①② | B、①③ | C、②③ | D、①②③ |
在△ABC中,三内角A,B,C的对边分别为a,b,c,面积为S,若S+a2=(b+c)2,则cosA等于( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
某程序框图如图所示,若该程序运行后输出的值是
,则( )

| 7 |
| 4 |

| A、a=3 | B、a=4 |
| C、a=5 | D、a=6 |
设不等式组
表示的平面区域为D,则区域D的面积为( )
|
| A、10 | B、15 | C、20 | D、25 |
双曲线
-
=1的右焦点到抛物线y2=4x的准线的距离为( )
| x2 |
| 4 |
| y2 |
| 12 |
| A、5 | B、4 | C、3 | D、2 |
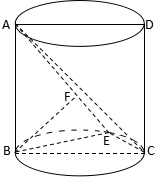 如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,BF⊥AE,F是垂足.
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,BF⊥AE,F是垂足.