题目内容
5.线段AD、BE分别时边长为2的等边三角形ABC在边BC、AC边上的高,则$\overrightarrow{AD}$•$\overrightarrow{BE}$=( )| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{3}}{2}$ |
分析 建立平面直角坐标系,求出A,D,E的坐标,得到$\overrightarrow{AD}$、$\overrightarrow{BE}$的坐标,从而求出$\overrightarrow{AD}$•$\overrightarrow{BE}$的值即可.
解答 解:以B为原点,$\overrightarrow{BC}$为x轴的正方向建立坐标系,
如图示: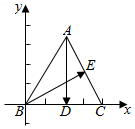 ,
,
等边三角形的边长是2,
故A(1,$\sqrt{3}$),D(1,0),E($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
∴$\overrightarrow{AD}$=(0,-$\sqrt{3}$),$\overrightarrow{BE}$=($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
∴$\overrightarrow{AD}$•$\overrightarrow{BE}$=0×$\frac{3}{2}$-$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=-$\frac{3}{2}$,
故选:A.
点评 本题考查了平面向量数量积的运算,考查数形结合思想,是一道中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目