题目内容
2.已知曲线C的参数方程为$\left\{\begin{array}{l}{x={t}^{2}+\frac{1}{{t}^{2}}-3}\\{y=2(t-\frac{1}{t})}\end{array}\right.$(t为参数)(1)将曲线C的参数方程化为普通方程;
(2)以原点为极点,x轴正方向为极轴,建立极坐标系,写出曲线C的极坐标方程.
分析 (1)分别用x,y表示出t2+$\frac{1}{{t}^{2}}$,t+$\frac{1}{t}$,利用完全平方公式消t得出x,y的关系,即曲线C的普通方程;
(2)将x=ρcosθ,y=ρsinθ代入普通方程得出极坐标方程.
解答 解:(1)由x=t2+$\frac{1}{{t}^{2}}$-3得t2+$\frac{1}{{t}^{2}}$=(t-$\frac{1}{t}$)2+2=x+3,
由y=2(t-$\frac{1}{t}$)得t-$\frac{1}{t}$=$\frac{y}{2}$,
∴曲线C的普通方程为($\frac{y}{2}$)2+2=x+3,即y2=4(x+1).
(2)∵x=ρcosθ,y=ρsinθ,
∴曲线C的极坐标方程是ρ2sin2θ=4(ρcosθ+1).
点评 本题考查了参数方程,极坐标方程与普通方程的转化,属于基础题.

练习册系列答案
相关题目
12.已知过定点P(2,0)的直线l与曲线$y=\sqrt{2-{x^2}}$相交于A,B两点,O为坐标原点,当△AOB的面积最大时,直线l的倾斜角为( )
| A. | 150° | B. | 135° | C. | 120° | D. | 30° |
7.设两条直线的方程分别为x+$\sqrt{3}$y+a=0,x+$\sqrt{3}$y+b=0,已知a,b是方程x2+2x+c=0的两个实根,且0≤c≤$\frac{1}{2}$,则这两条直线之间的距离的最大值和最小值的差为( )
| A. | $\frac{{2-\sqrt{2}}}{2}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{4-\sqrt{14}}}{4}$ |
11.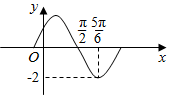 函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,则f($\frac{19π}{6}$)的值为( )
函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,则f($\frac{19π}{6}$)的值为( )
 函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,则f($\frac{19π}{6}$)的值为( )
函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,则f($\frac{19π}{6}$)的值为( )| A. | 0 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | -$\sqrt{2}$ |