题目内容
15．下面几种推理中是演绎推理的是（ ）| A． | 由金、银、铜、铁可导电，猜想：金属都可以导电 | |
| B． | 猜想数列5，7，9，11，…的通项公式为an=2n+3 | |
| C． | 由正三角形的性质得出正四面体的性质 | |
| D． | 半径为r的圆的面积S=π•r2，则单位圆的面积S=π |
分析 本题考查的是演绎推理的定义，判断一个推理过程是否是演绎推理关键是看他是否符合演绎推理的定义，能否从推理过程中找出“三段论”的三个组成部分．
解答 解：选项A是由特殊到一般的推理过程，为归纳推理，
选项B，是由特殊到一般的推理过程，为归纳推理，
选项C：是由特殊到与它类似的另一个特殊的推理过程，是类比推理，
选项D半径为r圆的面积S=πr2，因为单位圆的半径为1，则单位圆的面积S=π中，
半径为r圆的面积S=πr2，是大前提
单位圆的半径为1，是小前提
单位圆的面积S=π为结论．
故选：D．
点评 判断一个推理过程是否是归纳推理关键是看他是否符合归纳推理的定义，即是否是由特殊到一般的推理过程．
判断一个推理过程是否是类比推理关键是看他是否符合类比推理的定义，即是否是由特殊到与它类似的另一个特殊的推理过程．
判断一个推理过程是否是演绎推理关键是看他是否符合演绎推理的定义，能否从推理过程中找出“三段论”的三个组成部分．
练习册系列答案
相关题目
3．“e是无限不循环小数，所以e为无理数．”该命题是演绎推理中的三段论推理，其中大前提是（ ）
| A． | 无理数是无限不循环小数 | B． | 有限小数或有限循环小数为有理数 | ||
| C． | 无限不循环小数是无理数 | D． | 无限小数为无理数 |
10．
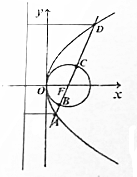如图，抛物线：y2=4mx（m＞0）和圆：x2+y2-2mx=0，直线l经过抛物线的焦点，依次交抛物线，圆于A，B，C，D四点，|AB|•|CD|=2，则m的值为（ ）
如图，抛物线：y2=4mx（m＞0）和圆：x2+y2-2mx=0，直线l经过抛物线的焦点，依次交抛物线，圆于A，B，C，D四点，|AB|•|CD|=2，则m的值为（ ）| A． | 2 | B． | $\sqrt{3}$ | C． | $\sqrt{2}$ | D． | 1 |
7．为了分析某次考试数学成绩情况，用简单随机抽样从某班中抽取40名学生的成绩作为样本，得到频率分布表如表：
（Ⅰ）求样本频率分布表中a，b的值，并根据上述频率分布表，在答题卡中作出样本频率分布直方图；
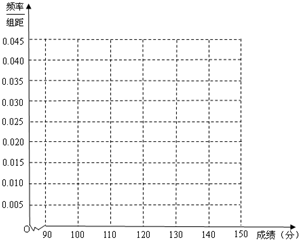
（Ⅱ）用样本估计总体，估计这个班这次数学成绩的平均数．（同一组中的数据用该组区间的中点值作代表）
| 分数 | [90，100） | [100，110） | [110，120） | [120，130） | [130，140） | [140，150] |
| 频数 | 2 | 8 | 12 | a | 6 | 2 |
| 频率 | 0.05 | 0.20 | 0.30 | b | 0.15 | 0.05 |
（Ⅱ）用样本估计总体，估计这个班这次数学成绩的平均数．（同一组中的数据用该组区间的中点值作代表）
4．过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点F作渐近线的垂线，设垂足为P（P为第一象限的点），延长FP交抛物线y2=2px（p＞0）于点Q，其中该双曲线与抛物线有一个共同的焦点，若$\overrightarrow{OP}$=$\frac{1}{2}$（$\overrightarrow{OF}$+$\overrightarrow{OQ}$），则双曲线的离心率的平方为（ ）
| A． | $\sqrt{5}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | $\sqrt{5}$+1 | D． | $\frac{\sqrt{5}+1}{2}$ |