题目内容
20.滕州市正在积极创建国家森林城市,为加快生态环境建设,每年用于改造生态环境总费用为x亿元,其中用于风景区改造的为y亿元.我市决定制定生态环境改造投资方案,该方案要求同时具备下列两个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得高于每年改造生态环境总费用的25%.若每年改造生态环境的总费用至少1亿元,至多4亿元,请你分析能否采用函数模型y=$\frac{1}{100}$(x3+4x+16)作为生态环境改造投资方案.分析 求导函数,可得函数的单调性,进而可求函数的最值,即可得到结论.
解答 解:∵y=$\frac{1}{100}$(x3+4x+16),
∴y′=$\frac{1}{100}(3{x}^{2}+4)$>0,
∴函数y=$\frac{1}{100}$(x3+4x+16)是增函数,满足条件①.
设g(x)=$\frac{y}{x}$=$\frac{1}{100}$(${x}^{2}+4+\frac{16}{x}$),
则g′(x)=$\frac{(x-2)({x}^{2}+2x+4)}{50{x}^{2}}$,
令g′(x)=0,得x=2.
当x<2时,g′(x)<0,g(x)在(-∞,2)上是减函数;
当x>2时,g′(x)>0,g(x)在(2,+∞)上是增函数,
又a=1,b=4,即x∈[1,2],g(x)在[1,2]上是减函数,在[1,4]上是增函数,
∴当x=2时,g(x)有最小值=16%>15%,
当x=4时,g(x)=24%<25%,x=1时,g(x)=25%≤25%.
∴能采用函数模型y=$\frac{1}{100}$(x3+4x+16)作为生态环境改造投资方案.
点评 本题考查利用数学知识解决实际问题,考查导数知识的运用,考查学生分析解决问题的能力,正确求导是关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
11.将函数f(x)=2sin(2x-$\frac{π}{4}$)的图象向左平移$\frac{π}{4}$个单位,得到函数g(x)的图象,则g(0)=( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 0 | D. | -$\sqrt{2}$ |
15.下面几种推理中是演绎推理的是( )
| A. | 由金、银、铜、铁可导电,猜想:金属都可以导电 | |
| B. | 猜想数列5,7,9,11,…的通项公式为an=2n+3 | |
| C. | 由正三角形的性质得出正四面体的性质 | |
| D. | 半径为r的圆的面积S=π•r2,则单位圆的面积S=π |
9.定义:如果函数f(x)在[a,b]上存在x1,x2(a<x1<x2<b)满足f'(x1)=$\frac{f(b)-f(a)}{b-a}$,f'(x2)=$\frac{f(b)-f(a)}{b-a}$,则称函数f(x)是[a,b]上的“双中值函数”,已知函数f(x)=2x3-x2+m是[0,2a]上“双中值函数”,则实数a的取值范围是( )
| A. | ($\frac{1}{8}$,$\frac{1}{4}$) | B. | ($\frac{1}{12}$,$\frac{1}{4}$) | C. | ($\frac{1}{12}$,$\frac{1}{8}$) | D. | ($\frac{1}{8}$,1) |
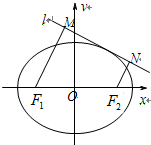 已知椭圆C的中心在坐标原点,左、右焦点分别为F1,F2,P为椭圆C上的动点,△PF1F2的面积最大值为$\sqrt{3}$,以原点为圆心,椭圆短半轴长为半径的圆与直线y=$\sqrt{3}$(x+2)相切.
已知椭圆C的中心在坐标原点,左、右焦点分别为F1,F2,P为椭圆C上的动点,△PF1F2的面积最大值为$\sqrt{3}$,以原点为圆心,椭圆短半轴长为半径的圆与直线y=$\sqrt{3}$(x+2)相切.