题目内容
6.在直角坐标系xOy中,圆x2+y2=4上一点P(x0,y0)(x0y0>0)处的切线l分别交x轴、y轴于点A,B,以A,B为顶点且以O为中心的椭圆记作C,直线OP交C于M,N两点.(Ⅰ)若P点坐标为($\sqrt{3}$,1),求椭圆C的离心率;
(Ⅱ)证明|MN|<4$\sqrt{2}$.
分析 (Ⅰ)运用直线的斜率公式,可得直线l的方程,求得A,B的坐标,可得椭圆的方程,运用离心率公式可得;
(Ⅱ)直线OP的斜率为k,依题意有k>0且k≠1,直线OP的方程为y=kx,直线l的方程为$y-{y_0}=-\frac{1}{k}({x-{x_0}})$,求得A,B的坐标,椭圆方程,代入直线y=kx,求得M,N的坐标,可得|OM|,运用基本不等式,即可得到结论.
解答 解:(Ⅰ)kOP=$\frac{1}{\sqrt{3}}$,可得k1=-$\sqrt{3}$,直线l的方程为y-1=-$\sqrt{3}$(x-$\sqrt{3}$),
令x=0,得y=4,令y=0,得x=$\frac{4\sqrt{3}}{3}$,可得A($\frac{4\sqrt{3}}{3}$,0)B(0,4).
即有椭圆C的方程为$\frac{3{x}^{2}}{16}$+$\frac{{y}^{2}}{16}$=1,
离心率e=$\frac{c}{a}$=$\sqrt{1-(\frac{b}{a})^{2}}$=$\frac{\sqrt{6}}{3}$;
(Ⅱ)证明:直线OP的斜率为k,依题意有k>0且k≠1,
直线OP的方程为y=kx,直线l的方程为$y-{y_0}=-\frac{1}{k}({x-{x_0}})$,
令x=0,得$y=\frac{x_0}{k}+{y_0}$,令y=0,得x=ky0+x0,
可得$A({k{y_0}+{x_0},0}),B({0,\frac{x_0}{k}+{y_0}})$,
椭圆C的方程$\frac{x^2}{{{{({k{y_0}+{x_0}})}^2}}}+\frac{y^2}{{{{({\frac{x_0}{k}+{y_0}})}^2}}}=1$,
联立$\left\{{\begin{array}{l}{y=kx}\\{\frac{x^2}{{{{({k{y_0}+{x_0}})}^2}}}+\frac{y^2}{{{{({\frac{x_0}{k}+{y_0}})}^2}}}=1}\end{array}}\right.$,
解出$x=±\frac{1}{{\sqrt{\frac{1}{{{{({k{y_0}+{x_0}})}^2}}}+\frac{k^2}{{{{({\frac{x_0}{k}+{y_0}})}^2}}}=1}}}=±\frac{{{x_0}+k{y_0}}}{{\sqrt{1+{k^4}}}}$,
可得$M({\frac{{{x_0}+k{y_0}}}{{\sqrt{1+{k^4}}}},k\frac{{{x_0}+k{y_0}}}{{\sqrt{1+{k^4}}}}})$,$N({-\frac{{{x_0}+k{y_0}}}{{\sqrt{1+{k^4}}}},-k\frac{{{x_0}+k{y_0}}}{{\sqrt{1+{k^4}}}}})$,
即有${|{OM}|^2}=\frac{{{{({{x_0}+k{y_0}})}^2}}}{{1+{k^4}}}+{k^2}\frac{{{{({{x_0}+k{y_0}})}^2}}}{{1+{k^4}}}=\frac{{1+{k^2}}}{{1+{k^4}}}{({{x_0}+k{y_0}})^2}$
=$\frac{{1+{{({\frac{y_0}{x_0}})}^2}}}{{1+{{({\frac{y_0}{x_0}})}^4}}}{({{x_0}+\frac{y_0}{x_0}{y_0}})^2}=\frac{{\frac{x_0^2+y_0^2}{x_0^2}}}{{\frac{x_0^4+y_0^4}{x_0^4}}}{({\frac{x_0^2+y_0^2}{x_0}})^2}=\frac{{4{{({x_0^2+y_0^2})}^2}}}{x_0^4+y_0^4}$
=$4({\frac{x_0^4+2x_0^2y_0^2+y_0^4}{x_0^4+y_0^4}})=4({1+\frac{2x_0^2y_0^2}{x_0^4+y_0^4}})=4({1+\frac{2}{{{{({\frac{x_0}{y_0}})}^2}+{{({\frac{y_0}{x_0}})}^2}}}})$
=4(1+$\frac{2}{{k}^{2}+\frac{1}{{k}^{2}}}$)<4(1+$\frac{2}{2}$)=8,
可得|OM|<2$\sqrt{2}$,
即有|MN|=2|OM|<4$\sqrt{2}$.
点评 本题考查椭圆的方程及运用,以及离心率公式,考查直线方程和椭圆方程联立,解方程求交点,考查化简整理的运算能力,属于难题.

 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案| A. | $\sqrt{2}$ | B. | 2 | C. | 0 | D. | -$\sqrt{2}$ |
| A. | 由金、银、铜、铁可导电,猜想:金属都可以导电 | |
| B. | 猜想数列5,7,9,11,…的通项公式为an=2n+3 | |
| C. | 由正三角形的性质得出正四面体的性质 | |
| D. | 半径为r的圆的面积S=π•r2,则单位圆的面积S=π |
| A. | y=2sin($\frac{2}{3}$x-$\frac{π}{9}$) | B. | y=2sin($\frac{2}{3}$x-$\frac{2π}{3}$) | C. | y=2sin($\frac{2}{3}$x-$\frac{5π}{9}$) | D. | y=2sin(6x-$\frac{7π}{3}$) |
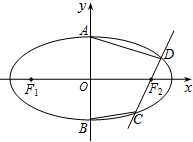 已知F1,F2分别是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左,右焦点,A,B分别为椭圆的上,下顶点.过椭圆的右焦点F2的直线在y轴右侧交椭圆于C,D两点.△F1CD的周长为8,且直线AC,BC的斜率之积为$-\frac{1}{4}$.
已知F1,F2分别是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左,右焦点,A,B分别为椭圆的上,下顶点.过椭圆的右焦点F2的直线在y轴右侧交椭圆于C,D两点.△F1CD的周长为8,且直线AC,BC的斜率之积为$-\frac{1}{4}$. 如图,F1,F2为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,D,E是椭圆的两个顶点,|F1F2|=2$\sqrt{3}$,|DE|=$\sqrt{5}$,若点M(x0,y0)在椭圆C上,则点N($\frac{{x}_{0}}{a}$,$\frac{{y}_{0}}{b}$)称为点M的一个“椭点”.直线l与椭圆交于A,B两点,A,B两点的“椭点”分别为P,Q,已知以PQ为直径的圆经过坐标原点O.
如图,F1,F2为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,D,E是椭圆的两个顶点,|F1F2|=2$\sqrt{3}$,|DE|=$\sqrt{5}$,若点M(x0,y0)在椭圆C上,则点N($\frac{{x}_{0}}{a}$,$\frac{{y}_{0}}{b}$)称为点M的一个“椭点”.直线l与椭圆交于A,B两点,A,B两点的“椭点”分别为P,Q,已知以PQ为直径的圆经过坐标原点O.