题目内容
求下列各式的值:
(1)(9
) -
;
(2)log2(log381)+lne2-lg1000+loga1(a>0且a≠1).
(1)(9
| 3 |
| 4 |
| 5 |
(2)log2(log381)+lne2-lg1000+loga1(a>0且a≠1).
考点:对数的运算性质
专题:函数的性质及应用
分析:(1)利用分数指数幂和根式的运算性质求解.
(2)利用对数的性质和运算法则求解.
(2)利用对数的性质和运算法则求解.
解答:
解:(1)(9
)-
=(32•3
)-
=(3
)-
=3-2=
.
(2)log2(log381)+lne2-lg1000+loga1
=log2(log334)+2lne-lg103+0=log24+2-3=2+2-3=1.
| 3 |
| 4 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
| 5 |
| 2 |
| 4 |
| 5 |
| 1 |
| 9 |
(2)log2(log381)+lne2-lg1000+loga1
=log2(log334)+2lne-lg103+0=log24+2-3=2+2-3=1.
点评:本题考查指数式和对数式化简求值,是基础题,解题时要注意指数和对数的性质的合理运用.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
在公比为正数的等比数列{an}中,a1+a2=2,a3+a4=8,则S8等于( )
| A、21 | B、42 |
| C、135 | D、170 |
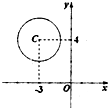 已知圆C:(x+3)2+(y-4)2=4
已知圆C:(x+3)2+(y-4)2=4 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°.平面ACEF⊥平面ABCD,四边形ACEF是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°.平面ACEF⊥平面ABCD,四边形ACEF是矩形,AE=a,点M在线段EF上.