题目内容
13.已知cos(α+$\frac{π}{6}$)=$\frac{\sqrt{3}}{3}$,则sin(2α-$\frac{π}{6}$)=$\frac{1}{3}$.分析 利用诱导公式化简已知可得sin(α-$\frac{π}{3}$)=-$\frac{\sqrt{3}}{3}$,由诱导公式及倍角公式化简所求可得sin(2α-$\frac{π}{6}$)=1-2sin2($α-\frac{π}{3}$),从而即可计算得解.
解答 解:∵cos(α+$\frac{π}{6}$)=sin[$\frac{π}{2}$-(α+$\frac{π}{6}$)]=sin($\frac{π}{3}$-α)=$\frac{\sqrt{3}}{3}$,可得:sin(α-$\frac{π}{3}$)=-$\frac{\sqrt{3}}{3}$,
∴sin(2α-$\frac{π}{6}$)=cos[$\frac{π}{2}$-(2α-$\frac{π}{6}$)]=cos[2($α-\frac{π}{3}$)]=1-2sin2($α-\frac{π}{3}$)=1-2×$\frac{3}{9}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 该题主要考查诱导公式和余弦的二倍角公式,还要求学生能够感受到 cos($\frac{π}{3}$-α) 与sin($\frac{π}{6}$+α) 中的角之间的余角关系,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.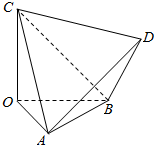 在如图所示的几何体中,三棱锥D-ABC的各条棱长均为2,OA,OB,OC两两垂直,则下列说法正确的是( )
在如图所示的几何体中,三棱锥D-ABC的各条棱长均为2,OA,OB,OC两两垂直,则下列说法正确的是( )
 在如图所示的几何体中,三棱锥D-ABC的各条棱长均为2,OA,OB,OC两两垂直,则下列说法正确的是( )
在如图所示的几何体中,三棱锥D-ABC的各条棱长均为2,OA,OB,OC两两垂直,则下列说法正确的是( )| A. | OA,OB,OC的长度可以不相等 | B. | 直线OB∥平面ACD | ||
| C. | 直线OD与BC所成的角是45° | D. | 直线AD与OB所成的角是45° |
8.下列四个函数中,与y=x表示同一函数的而是( )
| A. | y=$\frac{{x}^{2}}{x}$ | B. | y=$\sqrt{{x}^{2}}$ | C. | y=($\sqrt{x}$)2 | D. | y=$\root{3}{{x}^{3}}$ |
5.某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )


| A. | 72cm3 | B. | 90cm3 | C. | 108cm3 | D. | 138cm3 |