已知全集U=R.集合A={x|y=$\sqrt{2-x}$}.B={x|${2}^{-{x}^{2}+3x}$＞1}.则(∁UA)∩B=( )A．{x|2≤x＜3}B．{x|2＜x＜3}C．{x|x≥3}D．{x|2＜x≤3} 题目和参考答案——青夏教育精英家教网—

题目内容

15．已知全集U=R，集合A={x|y=$\sqrt{2-x}$}，B={x|${2}^{-{x}^{2}+3x}$＞1}，则（∁_UA）∩B=（　　）

A．

{x|2≤x＜3}

B．

{x|2＜x＜3}

C．

{x|x≥3}

D．

{x|2＜x≤3}

分析解根式不等式化简集合A，解指数不等式化简集合B，进一步求出A的补集，则（∁_UA）∩B的答案可求．

解答解：集合A={x|y=$\sqrt{2-x}$}={x|x≤2}，B={x|${2}^{-{x}^{2}+3x}$＞1}={x|0＜x＜3}，
∴∁_UA={x|x＞2}．
则（∁_UA）∩B={x|x＞2}∩{x|0＜x＜3}={x|2＜x＜3}．
故选：B．

点评本题考查了交、并、补集的混合运算，考查了不等式的解法，是基础题．

练习册系列答案

全景文化中考试题汇编3年真题2年模拟系列答案

金牌教练赢在燕赵系列答案

0系列答案

金题金卷热点测试系列答案

6．i是虚数单位，若$\frac{2+i}{1+i}$=a+bi（a，b∈R），则lg（a+b）的值是（　　）

3．已知函数f（x）=$\frac{1}{3}{x}^{3}-ax+4，（a＞0）$
（1）讨论函数 f （x）的单调性；
（2）若对任意的a∈[1，4），都存在x₀∈（2，3]使得不等式f（x₀）+e^a+2a＞m成立，求实数m 的取值范围．

10．（1）解方程：${log_3}（{{x^2}-3}）=1+{log_3}（x-\frac{5}{3}）$
（2）已知命题α：2≤x，命题β：|x-m|≤1，且命题α是β的必要条件，求实数m的取值范围．

20．已知有穷数列：${a_1}，{a_2}，{a_3}，…，{a_k}\;（k∈{N^*}，k≥3）$的各项均为正数，且满足条件：
①a₁=a_k；②${a_n}+\frac{2}{a_n}=2{a_{n+1}}+\frac{1}{{{a_{n+1}}}}\;\;（n=1，2，3，…，k-1）$．
（Ⅰ）若k=3，a₁=2，求出这个数列；
（Ⅱ）若k=4，求a₁的所有取值的集合；
（Ⅲ）若k是偶数，求a₁的最大值（用k表示）．

7．对任意正整数n，设a_n是方程x²+$\frac{x}{n}$=1的正根．求证：
（1）a_n+1＞a_n；
（2）$\frac{1}{2{a}_{2}}$+$\frac{1}{3{a}_{3}}$+…+$\frac{1}{n{a}_{n}}$＜1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$．

4．

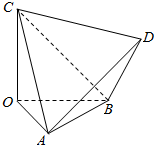在如图所示的几何体中，三棱锥D-ABC的各条棱长均为2，OA，OB，OC两两垂直，则下列说法正确的是（　　）

	A．	OA，OB，OC的长度可以不相等		B．	直线OB∥平面ACD
	C．	直线OD与BC所成的角是45°		D．	直线AD与OB所成的角是45°

5．某几何体的三视图（单位：cm）如图所示，则该几何体的体积是（　　）

试题分类