题目内容
15.在区间[0,π]上随机取一个数?,则使$\sqrt{2}≤\sqrt{2}cos?+\sqrt{2}$sin?≤2成立的概率为$\frac{1}{2}$.分析 利用三角函数的辅助角公式求出$\sqrt{2}$≤$\sqrt{2}$sinθ+$\sqrt{2}$cosθ≤2的等价条件,利用几何概型的概率公式即可得到结论.
解答 解:由$\sqrt{2}$≤$\sqrt{2}$sinθ+$\sqrt{2}$cosθ≤2,
得:$\frac{\sqrt{2}}{2}$≤sin(θ+$\frac{π}{4}$)≤1,
∵0≤θ≤π,
∴当0≤θ≤$\frac{π}{4}$,
则“$\sqrt{2}$≤$\sqrt{2}$sinθ+$\sqrt{2}$cosθ≤2”发生的概率P=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题主要考查几何概型的概率的计算,利用辅助角公式求出不等式的等价条件是解决本题的关键.

练习册系列答案
相关题目
6.设a=log54,b=log53,c=log45,则( )
| A. | a<c<b | B. | b<c<a | C. | a<b<c | D. | b<a<c |
3.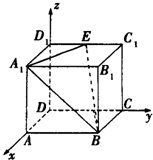 如图,在空间直角坐标系D-xyz中,四棱柱ABCD-A1B1C1D1为长方体,AA1=AB=2AD,点E为C1D1的中点,则二面角B1-A1B-E的余弦值为( )
如图,在空间直角坐标系D-xyz中,四棱柱ABCD-A1B1C1D1为长方体,AA1=AB=2AD,点E为C1D1的中点,则二面角B1-A1B-E的余弦值为( )
 如图,在空间直角坐标系D-xyz中,四棱柱ABCD-A1B1C1D1为长方体,AA1=AB=2AD,点E为C1D1的中点,则二面角B1-A1B-E的余弦值为( )
如图,在空间直角坐标系D-xyz中,四棱柱ABCD-A1B1C1D1为长方体,AA1=AB=2AD,点E为C1D1的中点,则二面角B1-A1B-E的余弦值为( )| A. | $-\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
10.设三条不同的直线l1,l2,l3满足l1⊥l3,l2⊥l3,则l1与l2( )
| A. | 是异面直线 | B. | 是相交直线 | ||
| C. | 是平行直线 | D. | 可能相交,或相交,或异面直线 |
20.已知y=lnx+x,x∈[1,e],则y的最大值为( )
| A. | 1 | B. | e-1 | C. | e+1 | D. | e |
7.要得到函数$y=\frac{{\sqrt{2}}}{2}sinx+\frac{{\sqrt{2}}}{2}cosx+1$的图象,需要把函数y=sinx的图象( )
| A. | 向右平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| B. | 向左平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| C. | 向左平移$\frac{π}{4}$个单位,再向下平移1个单位 | |
| D. | 向右平移$\frac{π}{4}$个单位,再向下平移1个单位 |
4.已知sinα+cosα=-$\frac{1}{5}$,α∈(0,π),则tanα的值为( )
| A. | -$\frac{4}{3}$或-$\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}$ |