题目内容
14.解方程:cos2x=cosx+sinx.分析 先化简方程,再利用三角函数的图象与性质,即可得出结论.
解答 解:∵cos2x=cosx+sinx,
∴cos2x-sin2x=cosx+sinx,
∴(cosx+sinx)(cosx-sinx)-(cosx+sinx)=0,
∴(cosx+sinx)(cosx-sinx-1)=0.
如果cosx+sinx=0,则得1+tanx=0,tanx=-1,
解x=kπ-$\frac{π}{4}$(k为整数).
如果cosx-sinx-1=0则得cosx-sinx=1,∴cos(x+$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$,
∴x+$\frac{π}{4}$=2kπ±$\frac{π}{4}$,∴x=2kπ或2kπ-$\frac{π}{2}$(k为整数).
综上,x=kπ-$\frac{π}{4}$或2kπ或2kπ-$\frac{π}{2}$(k为整数).
点评 本题是一个三角恒等变换问题,解题的关键是减小角的倍数,化异为同,利用方程的思想解题是三角函数常见的做法,最后是给值求角的问题,注意不要漏解.

练习册系列答案
相关题目
19.设f,g都是由A到A的映射,其对应法则如表所示(从上到下),则与f[g(1)]相同的是( )
表1 映射f的对应法则
表2 映射g的对应法则
表1 映射f的对应法则
| 原像 | 1 | 2 | 3 | 4 |
| 像 | 3 | 4 | 2 | 1 |
| 原像 | 1 | 2 | 3 | 4 |
| 像 | 4 | 3 | 1 | 2 |
| A. | g[f(3)] | B. | g[f(1)] | C. | f[f(4)] | D. | f[f(3)] |
6.设a=log54,b=log53,c=log45,则( )
| A. | a<c<b | B. | b<c<a | C. | a<b<c | D. | b<a<c |
3.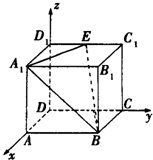 如图,在空间直角坐标系D-xyz中,四棱柱ABCD-A1B1C1D1为长方体,AA1=AB=2AD,点E为C1D1的中点,则二面角B1-A1B-E的余弦值为( )
如图,在空间直角坐标系D-xyz中,四棱柱ABCD-A1B1C1D1为长方体,AA1=AB=2AD,点E为C1D1的中点,则二面角B1-A1B-E的余弦值为( )
 如图,在空间直角坐标系D-xyz中,四棱柱ABCD-A1B1C1D1为长方体,AA1=AB=2AD,点E为C1D1的中点,则二面角B1-A1B-E的余弦值为( )
如图,在空间直角坐标系D-xyz中,四棱柱ABCD-A1B1C1D1为长方体,AA1=AB=2AD,点E为C1D1的中点,则二面角B1-A1B-E的余弦值为( )| A. | $-\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |