��Ŀ����
19����֪��ֱ������ϵxOy�У�����C�IJ�������Ϊ$\left\{\begin{array}{l}{x=2cos��}\\{y=2+2sin��}\end{array}\right.$����Ϊ���������ڼ�����ϵ����ֱ������ϵxOyȡ��ͬ�ij��ȵ�λ������ԭ��OΪ���㣬��x��������Ϊ���ᣩ�У�ֱ��l�ķ���Ϊ��cos����-$\frac{��}{4}$��=2$\sqrt{2}$������������C�ڼ�����ϵ�еķ��̣�
������ֱ��l������C�صõ��ҳ���
���� �����������C����ͨ���̣�����������C�ڼ�����ϵ�еķ��̣�
�������Բ�ĵ�ֱ�ߵľ��룬���ù��ɶ�����ֱ��l������C�صõ��ҳ���
��� �⣺��������C�IJ�������Ϊ$\left\{\begin{array}{l}{x=2cos��}\\{y=2+2sin��}\end{array}\right.$����Ϊ����������ͨ����Ϊx2+��y-2��2=4����x2+y2-4y=0��
������C�ڼ�����ϵ�еķ���Ϊ��=4sin�ȣ�
����ֱ��l�ķ���Ϊ��cos����-$\frac{��}{4}$��=2$\sqrt{2}$����x+y-4=0��
Բ�ĵ�ֱ�ߵľ���d=$\frac{|0+2-4|}{\sqrt{2}}$=$\sqrt{2}$��
��ֱ��l������C�صõ��ҳ�=2$\sqrt{4-2}$=2$\sqrt{2}$��
���� ���⿼�����ַ��̵Ļ���������㵽ֱ�߾��빫ʽ�����ã������е��⣮

��ϰ��ϵ�д�
�����Ŀ
10������y=��5x-3��3�ĵ����ǣ�������
| A�� | y'=3��5x-3��2 | B�� | y'=15��5x-3��2 | C�� | y'=9��5x-3��2 | D�� | y'=12��5x-3��2 |
14������$\frac{3-i}{1-i}$�ڸ�ƽ��������Ӧ�ĵ��ڵڣ����������ޣ�
| A�� | һ | B�� | �� | C�� | �� | D�� | �� |
3��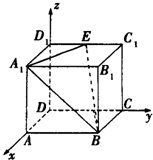 ��ͼ���ڿռ�ֱ������ϵD-xyz�У�������ABCD-A1B1C1D1Ϊ�����壬AA1=AB=2AD����EΪC1D1���е㣬������B1-A1B-E������ֵΪ��������
��ͼ���ڿռ�ֱ������ϵD-xyz�У�������ABCD-A1B1C1D1Ϊ�����壬AA1=AB=2AD����EΪC1D1���е㣬������B1-A1B-E������ֵΪ��������
 ��ͼ���ڿռ�ֱ������ϵD-xyz�У�������ABCD-A1B1C1D1Ϊ�����壬AA1=AB=2AD����EΪC1D1���е㣬������B1-A1B-E������ֵΪ��������
��ͼ���ڿռ�ֱ������ϵD-xyz�У�������ABCD-A1B1C1D1Ϊ�����壬AA1=AB=2AD����EΪC1D1���е㣬������B1-A1B-E������ֵΪ��������| A�� | $-\frac{{\sqrt{3}}}{3}$ | B�� | $-\frac{{\sqrt{3}}}{2}$ | C�� | $\frac{{\sqrt{3}}}{3}$ | D�� | $\frac{{\sqrt{3}}}{2}$ |
10����������ͬ��ֱ��l1��l2��l3����l1��l3��l2��l3����l1��l2��������
| A�� | ������ֱ�� | B�� | ���ֱཻ�� | ||
| C�� | ��ƽ��ֱ�� | D�� | �����ཻ�����ཻ��������ֱ�� |
7��Ҫ�õ�����$y=\frac{{\sqrt{2}}}{2}sinx+\frac{{\sqrt{2}}}{2}cosx+1$��ͼ����Ҫ�Ѻ���y=sinx��ͼ������
| A�� | ����ƽ��$\frac{��}{4}$����λ��������ƽ��1����λ | |
| B�� | ����ƽ��$\frac{��}{4}$����λ��������ƽ��1����λ | |
| C�� | ����ƽ��$\frac{��}{4}$����λ��������ƽ��1����λ | |
| D�� | ����ƽ��$\frac{��}{4}$����λ��������ƽ��1����λ |
8������{1��2}?A⊆{1��2��3��4��5��6}�ļ���A�ĸ����У�����������
| A�� | 13 | B�� | 14 | C�� | 15 | D�� | 16 |
