题目内容
11.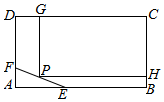 为了保护环境,实现城市绿化,某小区要在空地长方形ABCD上规划出一块长方形地面建造草坪CGPH,草坪一边落在CD上,一个顶点P在水池△AEF的边EF上,(如图,其中AB=200 m,BC=160m,AE=60m,AF=40m),设CG=xm,草坪的面积为f(x).
为了保护环境,实现城市绿化,某小区要在空地长方形ABCD上规划出一块长方形地面建造草坪CGPH,草坪一边落在CD上,一个顶点P在水池△AEF的边EF上,(如图,其中AB=200 m,BC=160m,AE=60m,AF=40m),设CG=xm,草坪的面积为f(x).(1)求函数y=f(x)的解析式,并写出它的定义域;
(2)求草坪面积的最大值,井求出此时CG的长度.(精确到整数)
分析 根据CG=x,矩形CGPH面积为f(x),作EN⊥PH于点N,因为三角形AEF∽三角形PEN,得到对应边成比例得到EN,用160-EN得到HC,然后利用矩形的面积求法,长乘以宽得到y与x的函数关系式,最后利用基本不等式求出最大值即可.
解答 解:(1)如图示: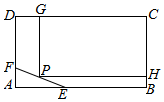
CG=x,矩形CGPH面积为f(x),
作EN⊥PH于点N,则 $\frac{EN}{40}$=$\frac{x-140}{60}$⇒EN=$\frac{2x-280}{3}$,
∴HC=160-$\frac{2x-280}{3}$=$\frac{760-2x}{3}$,
∴f(x)=x•$\frac{760-2x}{3}$=$\frac{1}{6}$•2x(760-2x),(140<x<200);
(2)由(1)得:f(x)=x•$\frac{760-2x}{3}$=$\frac{1}{6}$•2x(760-2x)≤$\frac{1}{2}$($\frac{760}{2}$)2=$\frac{72200}{3}$,
当2x=760-2x⇒x=190(m)即CG长为190m时,最大面积为 $\frac{72200}{3}$(m2).
点评 考查学生会根据实际问题选择合适的函数类型来解决实际问题,理解函数的最值及其几何意义.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
1.已知x,y满足不等式$\left\{\begin{array}{l}x-4y≤-3\\ 3x+5y≤25\\ x≥1\end{array}\right.$,则函数z=2x+y取得最大值是( )
| A. | 3 | B. | $\frac{13}{2}$ | C. | 12 | D. | 23 |
19.甲盒子里装有分别标有数字1,2,4,7的4张卡片,乙盒子里装有分别标有数字1,4的2张卡片,若从两个盒子中各随机地摸取出1张卡片,则2张卡片上的数字之积为奇数的概率为( )
| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
3.已知函敏f(x)=$\frac{1-2x}{1+x}$,函数y=g(x)的图象与y=f-1(x-1)的图象关于直线y=x对称,则y=g(x)的解析式为( )
| A. | $g(x)=\frac{3-2x}{x}$ | B. | $g(x)=\frac{2-x}{1+x}$ | C. | $g(x)=\frac{1-x}{2+x}$ | D. | $g(x)=\frac{3}{2+x}$ |
1.已知F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左,右焦点,点P在双曲线上,设PF1的中点在y轴上,且cos∠F1PF2=$\frac{1}{4}$,则双曲线的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{15}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{6}}{2}$ |