题目内容
14.函数f(x)=x2(x≥1)的反函数f-1(x)=$\sqrt{x}$(x≥1).分析 由y=x2(x≥1),解得x=$\sqrt{y}$(y≥1),把x与y互换即可得出.
解答 解:由y=x2(x≥1),解得x=$\sqrt{y}$(y≥1),把x与y互换可得:y=$\sqrt{x}$,
∴f(x)=x2(x≥1)的反函数f-1(x)=$\sqrt{x}$(x≥1).
故答案为:$\sqrt{x}$(x≥1).
点评 本题考查了反函数的求法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
4.若函数y=f(x)的导函数为y=f′(x),且f′(x)=sin2x-$\sqrt{3}$cos2x,则下列说法正确的是( )
| A. | y=f(x)的周期为$\frac{π}{2}$ | B. | y=f(x)在[0,$\frac{π}{6}$]上是减函数 | ||
| C. | y=f(x)的图象关于直线x=$\frac{π}{2}$对称 | D. | y=f(x)是偶函数 |
19.甲盒子里装有分别标有数字1,2,4,7的4张卡片,乙盒子里装有分别标有数字1,4的2张卡片,若从两个盒子中各随机地摸取出1张卡片,则2张卡片上的数字之积为奇数的概率为( )
| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
3.已知函敏f(x)=$\frac{1-2x}{1+x}$,函数y=g(x)的图象与y=f-1(x-1)的图象关于直线y=x对称,则y=g(x)的解析式为( )
| A. | $g(x)=\frac{3-2x}{x}$ | B. | $g(x)=\frac{2-x}{1+x}$ | C. | $g(x)=\frac{1-x}{2+x}$ | D. | $g(x)=\frac{3}{2+x}$ |
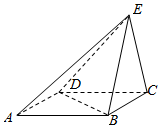 如图,ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.
如图,ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD. 已知圆C:(x-5)2+(y-7)2=4,一束光线从点A(-1,1)经x轴反射到圆周上,求光线的最短路程,并求此时的反射光线和入射光线的方程.
已知圆C:(x-5)2+(y-7)2=4,一束光线从点A(-1,1)经x轴反射到圆周上,求光线的最短路程,并求此时的反射光线和入射光线的方程.