题目内容
19.已知等差数列{an}中,a3a7=-16,a4+a6=0,求:(1)求{an}的通项公式;
(2){an}的前n项和Sn.
分析 (1)利用等差数列的通项公式即可得出.
(2)利用等差数列的求和公式即可得出.
解答 解 (1)设{an}的公差为d,a3a7=-16,a4+a6=0=a3+a7,
解得a3=4,a7=-4或a3=-4,a7=4.
∴a1+2d=4,a1+6d=-4,或a1+2d=-4,a1+6d=4.
解得$\left\{\begin{array}{l}{{a}_{1}=8}\\{d=-2}\end{array}\right.$或$\left\{\begin{array}{l}{{a}_{1}=-8}\\{d=2}\end{array}\right.$.
∴an=8-2(n-1)=10-2n,或an=-8+2(n-1)=2n-10.
(2)由(1)可得:$\left\{\begin{array}{l}{{a}_{1}=8}\\{d=-2}\end{array}\right.$或$\left\{\begin{array}{l}{{a}_{1}=-8}\\{d=2}\end{array}\right.$.
因此Sn=-8n+$\frac{n(n-1)}{2}×$2=n(n-9),或Sn=8n+$\frac{n(n-1)}{2}$×(-2)=-n(n-9).
点评 本题考查了等差数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.已知a,b∈R,定义运算“?”:a?b=$\left\{\begin{array}{l}{aa-b≤1}\\{ba-b>1}\end{array}\right.$,函数f(x)=(x2-2)?(x-1),x∈R,若方程f(x)-a=0只有两个不同实数根,则实数a的取值范围是( )
| A. | [-2,-1]∪(1,2) | B. | (-2,-1]∪(1,2] | C. | [-2,-1]∪[1,2] | D. | (-2,-1]∪(1,2) |
4.已知双曲线${x^2}-\frac{y^2}{2}=1$的焦点为F1,F2,则焦距|F1F2|=( )
| A. | 1 | B. | 2 | C. | $2\sqrt{3}$ | D. | 6 |
11.下列关系中正确的是( )
| A. | sin15°<sin163°<cos74° | B. | sin15°<cos74°<sin163° | ||
| C. | sin163°<sin15°<cos74° | D. | cos74°<sin163°<sin15° |
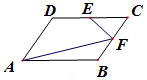 如图,菱形ABCD的边长为1,∠DAB=60°,E,F分别为DC、BC的中点,则$\overrightarrow{AF}•\overrightarrow{EF}$=$\frac{1}{8}$.
如图,菱形ABCD的边长为1,∠DAB=60°,E,F分别为DC、BC的中点,则$\overrightarrow{AF}•\overrightarrow{EF}$=$\frac{1}{8}$.