题目内容
12.极坐标系中,圆心在$(1,\frac{π}{4})$,半径为1的圆的方程为( )| A. | $ρ=2sin(θ-\frac{π}{4})$ | B. | $ρ=2cos(θ-\frac{π}{4})$ | C. | $ρcos(θ-\frac{π}{4})=2$ | D. | $ρsin(θ-\frac{π}{4})=2$ |
分析 由题意圆心在$(1,\frac{π}{4})$,半径为1的圆,利用直角坐标方程,先求得其直角坐标方程,间接求出所求圆的方程
解答 解:由题意可知,圆心在$(1,\frac{π}{4})$的直角坐标为($\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}$),半径为1.
得其直角坐标方程为(x-$\frac{\sqrt{2}}{2}$)2+(y-$\frac{\sqrt{2}}{2}$)2=1,即x2+y2=$\sqrt{2}$x+$\sqrt{2}$y
所以所求圆的极坐标方程是:ρ2=$\sqrt{2}ρ$cos$θ+\sqrt{2}ρ$sinθ=2ρcos($θ-\frac{π}{4}$).
故选B.
点评 本题考查了直角坐标化为极坐标方程,属于基础题

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
2.函数f(x)=x|x+a|+b是奇函数的充要条件是( )
| A. | ab=0 | B. | a+b=0 | C. | a2+b2=0 | D. | a=b |
7.已知函数y=f(x)的图象关于原点对称,且当x∈(-∞,0),f(x)+xf′(x)<0成立,若a=(-2)×f(-2),b=f(1),c=3×f(3),则a,b,c的关系大小是( )
| A. | b>a>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
17.已知函数f(x)=2-x2,g(x)=x.若f(x)*g(x)=min{f(x),g(x)},那么,f(x)*g(x)的最大值是( )(注:min表示最小值)
| A. | 2 | B. | 1 | C. | 0 | D. | $-\frac{1}{2}$ |
2.给出下列命题,正确的命题是( )
| A. | 底面是矩形的平行六面体是长方体 | |
| B. | 底面是正方形的直平行六面体是正四棱柱 | |
| C. | 底面是正方形的直四棱柱是正方体 | |
| D. | 所有棱长都相等的直平行六面体是正方体 |
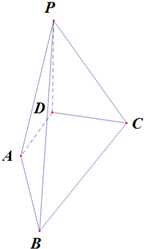 如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.