题目内容
7.已知函数y=f(x)的图象关于原点对称,且当x∈(-∞,0),f(x)+xf′(x)<0成立,若a=(-2)×f(-2),b=f(1),c=3×f(3),则a,b,c的关系大小是( )| A. | b>a>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
分析 构造函数F(x)=xf(x),求导数,判断单调性求解,再判断F(x)的奇偶性,即可得到F(-3)>F(-2)>F(-1),问题得以解决.
解答 解:令函数F(x)=xf(x),则F′(x)=f(x)+xf′(x)
∵f(x)+xf′(x)<0,
∴F(x)=xf(x)在(-∞,0)单调递减,
∵函数y=f(x)的图象关于原点对称,
∴y=f(x)是定义在R上的奇函数,
可知F(x)=xf(x)在R上为偶函数
∵a=-2f(-2),b=f(1),c=3•f(3),
∴a=F(-2),b=F(-1),c=F(-3)
∴F(-3)>F(-2)>F(-1),
即c>a>b
故选:C
点评 本题考察了复合函数的求导,导数在单调性中的应用,关键构造函数,掌握函数的奇偶性和单调性,属于中档题

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
12.极坐标系中,圆心在$(1,\frac{π}{4})$,半径为1的圆的方程为( )
| A. | $ρ=2sin(θ-\frac{π}{4})$ | B. | $ρ=2cos(θ-\frac{π}{4})$ | C. | $ρcos(θ-\frac{π}{4})=2$ | D. | $ρsin(θ-\frac{π}{4})=2$ |
19.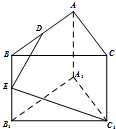 在正三棱柱ABC-A1B1C1中,AB=2,点D、E分别是棱AB、BB1的中点,若DE⊥EC1,则侧棱AA1的长为( )
在正三棱柱ABC-A1B1C1中,AB=2,点D、E分别是棱AB、BB1的中点,若DE⊥EC1,则侧棱AA1的长为( )
 在正三棱柱ABC-A1B1C1中,AB=2,点D、E分别是棱AB、BB1的中点,若DE⊥EC1,则侧棱AA1的长为( )
在正三棱柱ABC-A1B1C1中,AB=2,点D、E分别是棱AB、BB1的中点,若DE⊥EC1,则侧棱AA1的长为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
16.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点分别为F1,F2,点A在椭圆上,AF2⊥x轴,若$\frac{{|A{F_1}|}}{{|A{F_2}|}}=\frac{5}{3}$,则椭圆的离心率等于( )
| A. | 2 | B. | $\frac{1}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
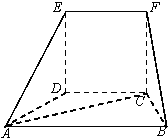 在如图的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.
在如图的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.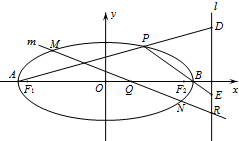 椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别是它的左、右焦点,已知椭圆C过点(0,1),且离心率e=$\frac{2\sqrt{2}}{3}$.
椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别是它的左、右焦点,已知椭圆C过点(0,1),且离心率e=$\frac{2\sqrt{2}}{3}$.