题目内容
3.已知函数f(x)=ax-lnx在($\frac{1}{2}$,+∞)上单调递增,则a的取值范围为[2,+∞).分析 求导函数,利用函数f(x)=ax-lnx在($\frac{1}{2}$,+∞)上单调递增,可得f′(x)≥0在($\frac{1}{2}$,+∞)上恒成立,分离参数,求出函数的最大值,即可求得实数a的取值范围.
解答 解:∵函数f(x)=ax-lnx在($\frac{1}{2}$,+∞)内单调递增,
∴当x>$\frac{1}{2}$时,f′(x)=a-$\frac{1}{x}$≥0,即a≥$\frac{1}{x}$,
∴a≥2,
即a的取值范围为[2,+∞),
故答案为:[2,+∞).
点评 本题主要考查利用导数研究函数的单调性,函数的单调性的性质,属于基础题.

练习册系列答案
相关题目
12.极坐标系中,圆心在$(1,\frac{π}{4})$,半径为1的圆的方程为( )
| A. | $ρ=2sin(θ-\frac{π}{4})$ | B. | $ρ=2cos(θ-\frac{π}{4})$ | C. | $ρcos(θ-\frac{π}{4})=2$ | D. | $ρsin(θ-\frac{π}{4})=2$ |
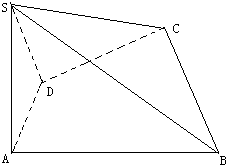 如图四棱锥S-ABCD,底面四边形ABCD满足条件∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,侧面SAD垂直于底面ABCD,SA=2,
如图四棱锥S-ABCD,底面四边形ABCD满足条件∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,侧面SAD垂直于底面ABCD,SA=2,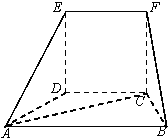 在如图的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.
在如图的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.