题目内容
2.函数f(x)=x|x+a|+b是奇函数的充要条件是( )| A. | ab=0 | B. | a+b=0 | C. | a2+b2=0 | D. | a=b |
分析 由奇函数的性质可得:f(0)=b=0,于是f(x)=x|x+a|,由f(-x)+f(x)=0,x≠0时,|x-a|=|x+a|恒成立,解得a=0.
解答 解:由奇函数的性质可得:f(0)=b=0,
∴f(x)=x|x+a|,
则f(-x)+f(x)=0,∴-x|-x+a|+x|x+a|=0,
x≠0时,|x-a|=|x+a|恒成立,则a=0.
∴函数f(x)=x|x+a|+b是奇函数的充要条件是a=b=0,即a2+b2=0.
故选:C.
点评 本题考查了函数的奇偶性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.随机变量ξ的分布列为:
随机变量ξ的方差D(ξ)1.
| ξ | 0 | 1 | 2 | 3 |
| P | x | 0.2 | 0.3 | 0.4 |
7.函数f(x)=x3+ax2+3x-1在x=-3时取得极值,则a=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
12.极坐标系中,圆心在$(1,\frac{π}{4})$,半径为1的圆的方程为( )
| A. | $ρ=2sin(θ-\frac{π}{4})$ | B. | $ρ=2cos(θ-\frac{π}{4})$ | C. | $ρcos(θ-\frac{π}{4})=2$ | D. | $ρsin(θ-\frac{π}{4})=2$ |
 的定义域为
的定义域为 ,值域为
,值域为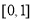 ,那么满足条件的整数对
,那么满足条件的整数对 共有( )
共有( )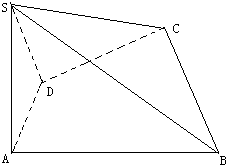 如图四棱锥S-ABCD,底面四边形ABCD满足条件∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,侧面SAD垂直于底面ABCD,SA=2,
如图四棱锥S-ABCD,底面四边形ABCD满足条件∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,侧面SAD垂直于底面ABCD,SA=2,