题目内容
设函数
.
（1）证明：
；
（2）设
为
的一个极值点，证明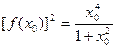
.
.（1）证明：
；（2）设
为的一个极值点，证明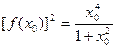.证明见解析
证明：1）
=
=
2)
① 又
②
由①②知
=
所以
=
= 2)
① 又 ②由①②知
= 所以
练习册系列答案
相关题目
题目内容
.；为的一个极值点，证明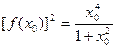.= ① 又 ②= 所以
，
.
，当
时比较
与
的大小关系.
，都有使得
，用反证法证明：
.
（
）的两边求导，得：
，
，化简得等式：
。
（
），证明：
。
，求证：
； （ii）
； （iii）
。
，是否存在不小于2的正整数
，使得对于任意的正整数
都能被
(n=1,2,…),求证：数列{cn}是等差数列；
、
，定义
，其中
是
、
、
，有如下四个命题：
；
；
；
.
，求证：
时，有
时，有
时，有
时，有
时，你能得到的结论是： ．
用反证法证明命题“
”,其反设正确的是
