题目内容
已知定义在R上的函数
，
定义：
.
(1)若
，当
时比较
与
的大小关系.
(2)若对任意的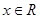
，都有使得
，用反证法证明：
.
，定义：
.(1)若
，当时比较与的大小关系.(2)若对任意的
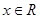，都有使得，用反证法证明：.（1）
；（2）见解析.
；（2）见解析.第一问中，利用因为，则
第二问，若
，则
的
则存在
使得
，
与矛盾，运用反证法得到结论。
解：（1）因为，则 --------6分
（2）若，则的
则存在使得，
与矛盾。所以假设不成立，原命题为真 -----------8分
，则第二问，若
，则的则存在
使得，与
矛盾，运用反证法得到结论。解：（1）因为
，则 --------6分（2）若
，则的则存在
使得，与
矛盾。所以假设不成立，原命题为真 -----------8分
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
.
；
为
的一个极值点，证明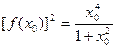
.
+
是无理数”时，假设正确的是（ ）
是有理数
或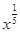
>
”时，假设的内容应该是 ．
个等式为 .（不必化简结果）
,
,
中恰有一个偶数”正确的反设为（ ）
，那么
”时，假设的内容应是
，如果
可被5整除，那么
，
至少有1个能被5整除．”则假设的内容是 （ ）
，求证:
，用反证法证明时，可假设
；
，
，求证:方程
的两根的绝对值都小于1．用反证法证明时可假设方程有一根
的绝对值大于或等于1，即假设
，以下结论正确的是（ ）
与
的假设都错误