题目内容
已知函数f(x)=2sin(ωx+φ)为偶函数(0<φ<π,ω>0),且函数y=f(x)图象的相邻对称轴的距离为
(1)求f(
)
(2)写出函数f(x)的单调减区间.
| π |
| 2 |
(1)求f(
| π |
| 8 |
(2)写出函数f(x)的单调减区间.
考点:正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:(1)由函数是偶函数求得φ,再由函数y=f(x)的图象的两相邻对称轴的距离为
求得函数周期,由周期公式求ω,则可求f(
);
(2)由2kπ≤2x≤2kπ+π,k∈Z可解得函数f(x)的单调减区间.
| π |
| 2 |
| π |
| 8 |
(2)由2kπ≤2x≤2kπ+π,k∈Z可解得函数f(x)的单调减区间.
解答:
解:(1)∵函数f(x)=2sin(ωx+φ)(0<φ<π,ω>0)为偶函数,
∴φ=
+kπ,k∈Z,
又0<φ<π,∴φ=
.
由函数y=f(x)的图象的两相邻对称轴的距离为
,得
=
,
∴T=π,则ω=2.
∴f(x)=2sin(2x+
)=2cos2x;
∴f(
)=2cos(2×
)=
.
(2)∵由2kπ≤2x≤2kπ+π,k∈Z可解得:kπ≤x≤kπ+
,k∈Z,
∴函数f(x)的单调减区间是:[kπ,kπ+
],k∈Z.
∴φ=
| π |
| 2 |
又0<φ<π,∴φ=
| π |
| 2 |
由函数y=f(x)的图象的两相邻对称轴的距离为
| π |
| 2 |
| T |
| 2 |
| π |
| 2 |
∴T=π,则ω=2.
∴f(x)=2sin(2x+
| π |
| 2 |
∴f(
| π |
| 8 |
| π |
| 8 |
| 2 |
(2)∵由2kπ≤2x≤2kπ+π,k∈Z可解得:kπ≤x≤kπ+
| π |
| 2 |
∴函数f(x)的单调减区间是:[kπ,kπ+
| π |
| 2 |
点评:本题考查了由y=Asin(ωx+φ)的部分图象求函数解析式,训练了复合函数单调性的求法,是中档题.

练习册系列答案
相关题目
已知集合A={x|x≤1},B={x|x2-2x<0}.则A∩B=( )
| A、(0,1] |
| B、[1,2) |
| C、(0,1) |
| D、(0,2) |
(1-
)5的展开式x2的系数是( )
| x |
| A、-5 | B、5 | C、-10 | D、10 |
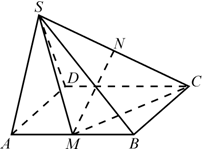 四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N分别是AB、SC的中点.
四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N分别是AB、SC的中点.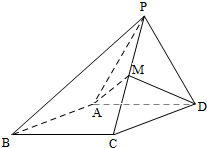 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.