题目内容
已知A(0,1,0)B(-1,0,-1)C(2,1,1)在xOz平面上是否存在一点使得PA⊥AB,PA⊥AC?若存在,求出P点坐标.
考点:向量的数量积判断向量的共线与垂直
专题:空间向量及应用
分析:假设在xOz平面上存在一点P(x,0,z)使得PA⊥AB,PA⊥AC,即
•
=
•
=0,解关于x和z的方程组可得.
| PA |
| AB |
| PA |
| AC |
解答:
解:假设在xOz平面上存在一点P(x,0,z)使得PA⊥AB,PA⊥AC,
∵A(0,1,0),B(-1,0,-1),C(2,1,1),
∴
=(-x,1,-z),
=(-1,-1,-1),
=(2,0,1),
∴
•
=x-1+z=0,
•
=-2x-z=0,
解得x=-1,z=2,∴P(-1,0,2)
∵A(0,1,0),B(-1,0,-1),C(2,1,1),
∴
| PA |
| AB |
| AC |
∴
| PA |
| AB |
| PA |
| AC |
解得x=-1,z=2,∴P(-1,0,2)
点评:本题考查空间向量的数量积和垂直关系,属基础题.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
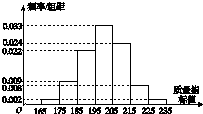 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得到如图所示的频率分布直方图.
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得到如图所示的频率分布直方图.