题目内容
5.已知A,B,C 是平面上不共线的三点,O是△ABC的重心,动点P满足$\overrightarrow{OP}$=$\frac{1}{3}$($\frac{1}{2}$$\overrightarrow{OA}$+$\frac{1}{2}$$\overrightarrow{OB}$+2$\overrightarrow{OC}$),则点P一定为三角形ABC的( )| A. | AB边中线的中点 | B. | AB边中线的三等分点(非重心) | ||
| C. | 重心 | D. | AB边的中点 |
分析 根据O是三角形的重心,得到三条中线上对应的向量的模长之间的关系,根据向量加法的平行四边形法则,求出向量的和,根据共线的向量的加减,得到结果.
解答 解:设AB 的中点是E,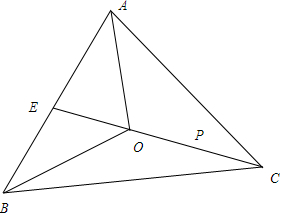
∵O是三角形ABC的重心,动点P满足$\overrightarrow{OP}$=$\frac{1}{3}$($\frac{1}{2}$$\overrightarrow{OA}$+$\frac{1}{2}$$\overrightarrow{OB}$+2$\overrightarrow{OC}$),
∴$\overrightarrow{OP}$=$\frac{1}{3}$($\overrightarrow{OE}$+2$\overrightarrow{OC}$)
∵$\overrightarrow{OC}$=2$\overrightarrow{EO}$,
∴$\overrightarrow{OP}$=$\frac{1}{3}$($\overrightarrow{OE}+4\overrightarrow{EO}$)=$\frac{1}{3}×3\overrightarrow{EO}$=$\overrightarrow{EO}$,
∴P在AB边的中线上,是中线的三等分点,不是重心.
故选:B.
点评 本题考查三角形的重心,考查向量加法的平行四边形法则,考查故选向量的加减运算,是一个比较简单的综合题目,这种题目可以以选择或填空出现.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.函数f(x)=|sinx+2cosx|+|2sinx-cosx|的最小正周期为( )
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
13.我国从2016年1月1日起统一实施全面两孩政策.为了解适龄民众对放开生育二胎政策的态度,某市选取70后和80后作为调查对象,随机调查了100位,得到数据如表:
(1)以这100个人的样本数据估计该市的总体数据,且视频率为概率,若从该市70后公民中随机抽取3位,记其中生二胎的人数为X,求随机变量X的分布列,数学期望和方差;
(2)根据调查数据,是否有90%的把握认为“生二胎与年龄有关”,并说明理由.
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| 生二胎 | 不生二胎 | 合计 | |
| 70后 | 30 | 15 | 45 |
| 80后 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
(2)根据调查数据,是否有90%的把握认为“生二胎与年龄有关”,并说明理由.
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
20.已知f(x)=2xf′(1)+lnx,则f′(1)=( )
| A. | -e | B. | -1 | C. | 1 | D. | e |
17.某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩如表所示:
若单科成绩85以上(含85分),则该科成绩优秀.
(1)根据上表完成下面的2×2的列联表(单位:人)
(2)能否判断是否有99%的把握性认为,学生的数学成绩与物理成绩有关系?
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 92 | 81 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | 5 | 2 | 7 |
| 物理成绩不优秀 | 1 | 12 | 13 |
| 合计 | 6 | 14 | 20 |
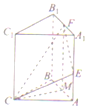 在三棱柱ABC-A1B1C1中,已知侧按AA1⊥底面ABC,且四边形AA1B1B是边长为2的正方形,CA=CB,点M为棱AB的中点,点E,F分别在按AA1,A1B1上
在三棱柱ABC-A1B1C1中,已知侧按AA1⊥底面ABC,且四边形AA1B1B是边长为2的正方形,CA=CB,点M为棱AB的中点,点E,F分别在按AA1,A1B1上