题目内容

函数f（x）=
2-lg(3-x)
的定义域为
 
．
考点：指、对数不等式的解法
专题：函数的性质及应用
分析：根据函数的结构列出限制条件，求解不等式组得到定义域．
解答： 解：由题意知
2-lg(3-x)≥0
3-x＞0
，
解得：-97≤x＜3，
所以函数的定义域为[-97，3），
故答案为：[-97，3）．
点评：本题考查函数定义域的求解，其中有对数不等式的求解，注意应先将实数化为同底的对数，再利用对数函数的单调性求解．属基础题．
练习册系列答案
相关题目
写出与下列各角终边相同的角的集合，并把集合中适合不等式-360°≤β＜360°的元素β写出来：
（1）60°   （2）-75°   （3）-824°30′（4）475°
（5）90°   （6）270°   （7）180°       （8）0°．
若角α满足180°＜α＜360°，角5α与α有相同的始边，且有相同的终边，则角α=
 
．
若a∈R，求函数f（x）=x+
a
x
分别在下列区间上的值域．
（1）（0，3]；
（2）[5，+∞）
已知F1、F2分别是椭圆M：
x2
a2
+
y2
a2-2
=1（a＞
2
）的左右焦点，点P是椭圆M上一点，且
PF1
•
PF2
=0，则离心率e取最小值时椭圆M的方程为（　　）
A、
x2
8
+
y2
6
=1
B、
x2
4
+
y2
2
=1
C、
x2
6
+
y2
4
=1
D、
x2
16
+
y2
14
=1
已知一圆锥曲线上任意一点P（x，y）满足
x2+(y-4)2
+
x2+(y+4)2
=10，请将此方程化为圆锥曲线的标准方程．
以下给出五个命题，其中真命题的序号为
 

①函数f（x）=3ax+1-2a在区间（-1，1）上存在一个零点，则a的取值范围是a＜-1或a＞
1
5
；
②“菱形的对角线相等”的否定是“菱形的对角线不相等”；
③?x∈（0，
π
2
），x＜tanx；
④若0＜a＜b＜1，则lna＜lnb＜ab＜ba；
⑤“b2=ac”是“a，b，c成等比数列”的充分不必要条件．
已知不等式ax2+bx-2＞0的解集是{x|-2＜x＜-
1
4
}，则a-b=
 
．
已知图1、图2分别表示A、B两城市某月1日至6日当天最低气温的数据折线图（其中横轴n表示日期，纵轴x表示气温），记A、B两城市这6天的最低气温平均数分别为
.
xA
和
.
xB
，标准差分别为sA和sB，则它们的大小关系是（　　）
A、
.
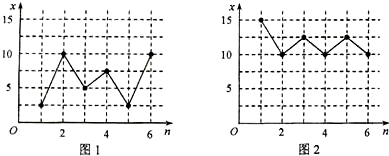
xA
＞
.
xB
，sA＞sB
B、
.
xA
＞
.
xB
，sA＜sB
C、
.
xA
＜
.
xB
，sA＜sB
D、
.
xA
＜
.
xB
，sA＞sB

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网