题目内容
18．
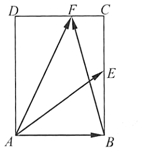如图，在矩形ABCD中，AB=$\sqrt{2}$，BC=2，点E为BC的中点，点F在边CD上，若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$，则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是（ ）| A． | 2-$\sqrt{2}$ | B． | 1 | C． | $\sqrt{2}$ | D． | 2 |
分析 根据题意，可分别以边AB，AD所在直线为x轴，y轴，建立平面直角坐标系，然后可得出点A，B，E的坐标，并设F（x，2），根据$\overrightarrow{AB}•\overrightarrow{AF}=\sqrt{2}$即可求出x值，从而得出F点的坐标，从而求出$\overrightarrow{AE}•\overrightarrow{BF}$的值．
解答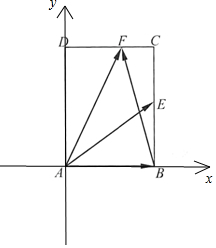 
解：据题意，分别以AB、AD所在直线为x，y轴，
建立如图所示平面直角坐标系，则：
A（0，0），B（$\sqrt{2}$，0），E（$\sqrt{2}$，1），设F（x，2）；
∴$\overrightarrow{AB}•\overrightarrow{AF}=（\sqrt{2}，0）•（x，2）=\sqrt{2}x=\sqrt{2}$；
∴x=1；
∴F（1，2），$\overrightarrow{AE}=（\sqrt{2}，1），\overrightarrow{BF}=（1-\sqrt{2}，2）$；
∴$\overrightarrow{AE}•\overrightarrow{BF}=\sqrt{2}-2+2=\sqrt{2}$．
故选C．
点评 考查通过建立平面直角坐标系，利用坐标解决向量问题的方法，向量数量积的坐标运算．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
8．若平面内三点A（1，-a），B（2，a2），C（3，a3）共线，则a=（ ）
| A． | 1±$\sqrt{2}$或0 | B． | $\frac{{2-\sqrt{5}}}{2}或0$ | C． | $\frac{{2±\sqrt{5}}}{2}$ | D． | $\frac{{2+\sqrt{5}}}{2}或0$ |
9．直线x=$\frac{π}{4}$和x=$\frac{5π}{4}$是函数f（x）=sin（ωx+φ）图象的两条相邻的对称轴，则φ的值为（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{2}$ | D． | $\frac{3π}{4}$ |
6．已知集合A={x|y=lg（x-1）}，B={x||x|＜2}，则A∩B=（ ）
| A． | （-2，0） | B． | （0，2） | C． | （1，2） | D． | （-2，2） |
5．在△ABC中，AB=2，AC=3，$\overrightarrow{AB}•\overrightarrow{BC}=1$，则$|\overrightarrow{BC}|$=（ ）
| A． | $\sqrt{7}$ | B． | $\sqrt{3}$ | C． | 2$\sqrt{2}$ | D． | $\sqrt{23}$ |