题目内容
5.在△ABC中,AB=2,AC=3,$\overrightarrow{AB}•\overrightarrow{BC}=1$,则$|\overrightarrow{BC}|$=( )| A. | $\sqrt{7}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{23}$ |
分析 根据$\overrightarrow{BC}$=$\overrightarrow{AC}-\overrightarrow{AB}$和$\overrightarrow{AB}•\overrightarrow{BC}=1$计算$\overrightarrow{AB}•\overrightarrow{AC}$,再计算($\overrightarrow{AC}-\overrightarrow{AB}$)2即可得出答案.
解答 解:∵$\overrightarrow{AB}•\overrightarrow{BC}$=$\overrightarrow{AB}•(\overrightarrow{AC}-\overrightarrow{AB})$=$\overrightarrow{AB}•\overrightarrow{AC}$-${\overrightarrow{AB}}^{2}$=1,
∴$\overrightarrow{AB}•\overrightarrow{AC}$=1+${\overrightarrow{AB}}^{2}$=1+4=5,
∴${\overrightarrow{BC}}^{2}$=($\overrightarrow{AC}-\overrightarrow{AB}$)2=${\overrightarrow{AC}}^{2}$-2$\overrightarrow{AB}•\overrightarrow{AC}$+${\overrightarrow{AB}}^{2}$=3,
∴|$\overrightarrow{BC}$|=$\sqrt{3}$,
故选B.
点评 本题考查了平面向量的模长计算,数量积运算,属于中档题.

练习册系列答案
相关题目
17.直线y=a与y=2x-3及曲线y=x+ex分别交于A、B两点,则|AB|的最小值为( )
| A. | $\frac{3}{2}$ | B. | e | C. | 3 | D. | 2 |
18.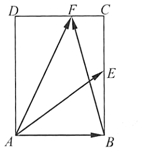 如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是( )
如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是( )
 如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是( )
如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是( )| A. | 2-$\sqrt{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
13.已知一空间几何体的三视图如图所示,其中俯视图为正方形,则该几何体的外接球的表面积为( )


| A. | 27π | B. | 49π | C. | 81π | D. | 100π |
20.下列关于命题的说法中错误的是( )
| A. | 对于命题p:?x∈R,使得x2+x+1<0,则¬P:?x∈R,均有x2+x+1≥0 | |
| B. | “x=1”是“x2-4x+3=0”的充分不必要条件 | |
| C. | 命题“若x2-4x+3=0,则x=1”的逆否命题为“若x≠1,则x2-4x+3≠0” | |
| D. | 若p∧q为假命题,则p、q均为假命题 |
15.已知集合A={0,1,2,3,4},集合B={x|x=2n,n∈A},则A∩B=( )
| A. | {0} | B. | {0,2,4} | C. | {2,4} | D. | {0,2} |
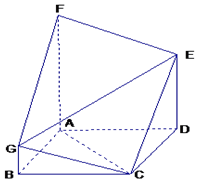 如图,多面体ABCDEFG中,四边形ABCD是正方形,FA⊥平面ABCD,
如图,多面体ABCDEFG中,四边形ABCD是正方形,FA⊥平面ABCD,