题目内容

8．若平面内三点A（1，-a），B（2，a2），C（3，a3）共线，则a=（　　）
A．1±$\sqrt{2}$或0B．$\frac{{2-\sqrt{5}}}{2}或0$C．$\frac{{2±\sqrt{5}}}{2}$D．$\frac{{2+\sqrt{5}}}{2}或0$

分析 平面内三点A（1，-a），B（2，a2），C（3，a3）共线，可得kAB=kAC．利用斜率计算公式即可得出．

解答 解：∵平面内三点A（1，-a），B（2，a2），C（3，a3）共线，∴kAB=kAC．
∴$\frac{{a}^{2}+a}{2-1}=\frac{{a}^{3}+a}{3-1}$，化为：a（a2-2a-1）=0，
解得a=0或a=$1±\sqrt{2}$．
故选：A．

点评 本题考查了三点共线与斜率的计算公式，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
18．若二次函数y=x2+2x+（m+3）有两个不同的零点，则m的取值范围是（　　）
A．（-∞，-2）B．（-∞，-2]C．（-∞，4）D．（4，+∞）
19．已知椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）离心率为$\frac{\sqrt{6}}{3}$，焦距为2$\sqrt{2}$，抛物线C2：x2=2py（p＞0）的焦点F是椭圆C1的顶点．
（Ⅰ）求C1与C2的标准方程；
（Ⅱ）设过点F的直线l交C2于P，Q两点，若C1的右顶点A在以PQ为直径的圆内，求直线l的斜率的取值范围．
16．已知函数$f（x）=2sin（wx+φ+\frac{π}{3}）+1（|φ|＜\frac{π}{2}，w＞0）$是偶函数，且函数f（x）两相邻对称轴之间的距离为$\frac{π}{2}$．
（1）求$f（\frac{π}{8}）$的值．
（2）当x∈（-$\frac{π}{2}$，$\frac{3π}{2}$）时，求方程f（x）=$\frac{5}{4}$的实数根之和．
3．偶函数f（x）在（0，+∞）上递增，a=f（log2$\frac{1}{3}$）b=f（$\frac{3}{2}$）c=f（log32），则下列关系式中正确的是（　　）
A．＜b＜cB．a＜c＜bC．c＜a＜bD．c＜b＜a
13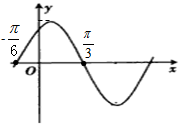．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象向左平移$\frac{π}{12}$单位得到的部分图象如图，则φ=（　　）
A．$\frac{π}{6}$B．-$\frac{π}{6}$C．$\frac{2π}{3}$D．$\frac{π}{2}$
20．如图，某组合体的三视图是由边长为2的正方形和直径为2的圆组成，则它的体积为（　　）
A．4+4πB．8+4πC．$4+\frac{4}{3}π$D．$8+\frac{4}{3}π$
17．直线y=a与y=2x-3及曲线y=x+ex分别交于A、B两点，则|AB|的最小值为（　　）
A．$\frac{3}{2}$B．eC．3D．2
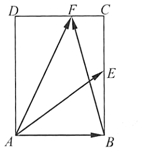18．如图，在矩形ABCD中，AB=$\sqrt{2}$，BC=2，点E为BC的中点，点F在边CD上，若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$，则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是（　　）
A．2-$\sqrt{2}$B．1C．$\sqrt{2}$D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网