题目内容
13.已知曲线y=5$\sqrt{2x+1}$,求:(1)曲线在x=0处的切线方程;
(2)曲线上与直线5x-2y+1=0平行的切线的方程.
分析 (1)求导数,确定切线的斜率,求得切点坐标,进而可求曲线在x=0处的切线方程;
(2)由题意得$\frac{5}{\sqrt{2{x}_{0}+1}}$=$\frac{5}{2}$,求得切点坐标,进而可求曲线上与直线5x-2y+1=0平行的切线的方程.
解答 解:y′=(5$\sqrt{2x+1}$)′=5•$\frac{1}{2}$$(2x+1)^{-\frac{1}{2}}$•(2x+1)′=$\frac{5}{\sqrt{2x+1}}$.
(1)当x=0时导数值为5,所以曲线y=5$\sqrt{2x+1}$在x=0处的切线的斜率为k=5,
又切点坐标为(0,5),所以切线方程为y-5=5x,即5x-y+5=0.
(2)设切点坐标为(x0,y0),则切线斜率为$\frac{5}{\sqrt{2{x}_{0}+1}}$.
由题意得$\frac{5}{\sqrt{2{x}_{0}+1}}$=$\frac{5}{2}$.∴x0=$\frac{3}{2}$,切点坐标为($\frac{3}{2}$,10),
∴切线方程为y-10=$\frac{5}{2}$(x-$\frac{3}{2}$),
即为10x-4y+25=0.
点评 本题考查导数知识的运用,考查导数的几何意义,求出切线的斜率是关键,属于中档题.

练习册系列答案
相关题目
3.偶函数f(x)在(0,+∞)上递增,a=f(log2$\frac{1}{3}$)b=f($\frac{3}{2}$)c=f(log32),则下列关系式中正确的是( )
| A. | <b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
1.设计一个计算1×3×5×7×9的算法,下面给出了算法语句的一部分,则在横线①上应填入下面数据中的( )

| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
18.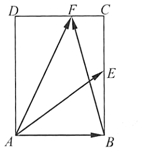 如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是( )
如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是( )
 如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是( )
如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是( )| A. | 2-$\sqrt{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
3.若sinα+cosα=tan390°,则sin2α等于( )
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
20.下列关于命题的说法中错误的是( )
| A. | 对于命题p:?x∈R,使得x2+x+1<0,则¬P:?x∈R,均有x2+x+1≥0 | |
| B. | “x=1”是“x2-4x+3=0”的充分不必要条件 | |
| C. | 命题“若x2-4x+3=0,则x=1”的逆否命题为“若x≠1,则x2-4x+3≠0” | |
| D. | 若p∧q为假命题,则p、q均为假命题 |
1.过点P(1,0)与抛物线y=x2有且只有一个公共点的直线共有( )
| A. | 4条 | B. | 3条 | C. | 2条 | D. | 1条 |