题目内容
9.直线x=$\frac{π}{4}$和x=$\frac{5π}{4}$是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,则φ的值为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
分析 根据直线x=$\frac{π}{4}$和x=$\frac{5π}{4}$是函数图象中相邻的两条对称轴,可得$\frac{1}{2}$T=$\frac{5π}{4}-\frac{π}{4}$,可得ω.根据对称轴方程求解φ的关系式,根据k∈Z.可得φ的值.
解答 解:由题意,直线x=$\frac{π}{4}$和x=$\frac{5π}{4}$是函数图象中相邻的两条对称轴,
∴$\frac{5π}{4}$-$\frac{π}{4}$=$\frac{T}{2}$,即$\frac{T}{2}$=π,可得T=2π.
又∵T=$\frac{2π}{ω}$=2π,
∴ω=1,
故得f(x)=sin(x+φ).
∵直线x=$\frac{π}{4}$是函数图象的对称轴,
∴$\frac{π}{4}$+φ=$\frac{π}{2}$+kπ,k∈Z,
∴φ=$\frac{π}{4}$+kπ,k∈Z.
当k=0时,可得φ=$\frac{π}{4}$,检验知,当l=1时,此时直线x=$\frac{5π}{4}$也为对称轴.
故选A.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.如图,某组合体的三视图是由边长为2的正方形和直径为2的圆组成,则它的体积为( )


| A. | 4+4π | B. | 8+4π | C. | $4+\frac{4}{3}π$ | D. | $8+\frac{4}{3}π$ |
17.直线y=a与y=2x-3及曲线y=x+ex分别交于A、B两点,则|AB|的最小值为( )
| A. | $\frac{3}{2}$ | B. | e | C. | 3 | D. | 2 |
1.设计一个计算1×3×5×7×9的算法,下面给出了算法语句的一部分,则在横线①上应填入下面数据中的( )

| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
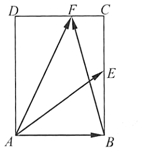 如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是( )
如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是( )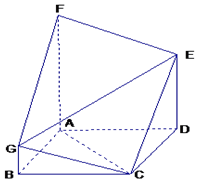 如图,多面体ABCDEFG中,四边形ABCD是正方形,FA⊥平面ABCD,
如图,多面体ABCDEFG中,四边形ABCD是正方形,FA⊥平面ABCD,