题目内容
12.函数f(x)=x3+mx2+nx+1(m,n∈R)在区间[1,2]上单调递增,则3m+n的最小值为-$\frac{15}{2}$.分析 求导数,利用f(x)=x3+mx2+nx+1(m,n∈R)在区间[1,2]上单调递增,3x2+2mx+n≥0在区间[1,2]上恒成立,可得$\left\{\begin{array}{l}{2m+n≥-3}\\{4m+n≥-12}\end{array}\right.$,利用3m+n=$\frac{1}{2}$(2m+n+4m+n),即可得出结论.
解答 解:∵f(x)=x3+mx2+nx+1,
∴f′(x)=3x2+2mx+n,
∵f(x)=x3+mx2+nx+1(m,n∈R)在区间[1,2]上单调递增,
∴3x2+2mx+n≥0在区间[1,2]上恒成立,
∴$\left\{\begin{array}{l}{3+2m+n≥0}\\{12+4m+n≥0}\end{array}\right.$,∴$\left\{\begin{array}{l}{2m+n≥-3}\\{4m+n≥-12}\end{array}\right.$,
∴3m+n=$\frac{1}{2}$(2m+n+4m+n)≥-$\frac{15}{2}$,
∴3m+n的最小值为-$\frac{15}{2}$.
故答案为:-$\frac{15}{2}$.
点评 本题考查函数的单调性,考查导数知识的综合运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
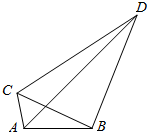 如图,△ABC与△CBD都是直角三角形,∠BAC=∠DBC=90°,∠ABC=∠BDC=30°,若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,求x,y的值.
如图,△ABC与△CBD都是直角三角形,∠BAC=∠DBC=90°,∠ABC=∠BDC=30°,若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,求x,y的值.