题目内容
定义在R上的奇函数f(x)满足:当x>0时,f(x)=-log2x,则f(f(-
))= .
| 1 |
| 4 |
考点:函数奇偶性的性质,函数的值
专题:函数的性质及应用
分析:利用奇函数的性质和对数函数的性质结合已知条件直接求解.
解答:
解:∵定义在R上的奇函数f(x)满足:当x>0时,f(x)=-log2x,
∴f(-
)=-f(
)=log2
=-2,
∴f(f(-
))=f(-2)=-f(2)=log22=1.
故答案为:1.
∴f(-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
∴f(f(-
| 1 |
| 4 |
故答案为:1.
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意奇函数的性质和对数函数的性质的合理运用.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
两直线3x+y-3=0与ax+2y-1=0垂直,则a=( )
| A、-6 | ||
| B、6 | ||
C、-
| ||
D、
|
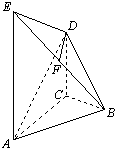 在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.
在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.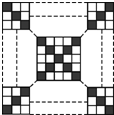 如图所示,在一个(2n-1)×(2n-1)(n∈N且n≥2)的正方形网格内涂色,要求两条对角线的网格涂黑色,其余网格涂白色.若用f(n)表示涂白色网格的个数与涂黑色网格的个数的比值,则f(n)的最小值为
如图所示,在一个(2n-1)×(2n-1)(n∈N且n≥2)的正方形网格内涂色,要求两条对角线的网格涂黑色,其余网格涂白色.若用f(n)表示涂白色网格的个数与涂黑色网格的个数的比值,则f(n)的最小值为