题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,且A=45°,C=30°,a=
.
(1)求c的值;
(2)求△ABC的面积.
| 2 |
(1)求c的值;
(2)求△ABC的面积.
考点:正弦定理
专题:计算题,解三角形
分析:(1)由正弦定理得c=
,把已知代入即可求值.
(2)根据已知先求sinB的值,从而可求△ABC的面积.
| asinC |
| sinA |
(2)根据已知先求sinB的值,从而可求△ABC的面积.
解答:
解:(1)由正弦定理,得
=
…(2分)
∴c=
…(3分)
把A=45°,C=30°,a=
代入上式,得c=
=
=1…(6分)
(2)∵B=180°-(A+C)=180°-(45°+30°)=105°…(7分)
∴sinB=sin105°=sin(45°+60°)=sin45°cos60°+cos45°sin60°…(9分)=
×
+
×
=
…(10分)
∴△ABC的面积S△ABC=
acsinB=
×
×1×
=
…(12分)
(也可先用余弦定理求b=
,再求面积)
| a |
| sinA |
| c |
| sinC |
∴c=
| asinC |
| sinA |
把A=45°,C=30°,a=
| 2 |
| ||
| sin45° |
| ||||
|
(2)∵B=180°-(A+C)=180°-(45°+30°)=105°…(7分)
∴sinB=sin105°=sin(45°+60°)=sin45°cos60°+cos45°sin60°…(9分)=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||||
| 4 |
∴△ABC的面积S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||||
| 4 |
1+
| ||
| 4 |
(也可先用余弦定理求b=
| ||||
| 2 |
点评:此题考查了正弦定理,以及三角形的面积公式,熟练掌握定理及公式是解本题的关键,属于基本知识的考查.

练习册系列答案
相关题目
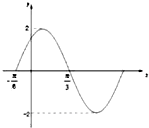
如图是函数f(x)=Asin(ωx+φ)的部分图象,则f(x)的表达式为( )

A、f(x)=2sin(2x-
| ||
B、f(x)=2sin(2x+
| ||
C、f(x)=2sin(x+
| ||
D、f(x)=2sin(2x-
|
当y=f(x)是下列的( )时,f′(x)一定是增函数.
| A、二次函数 | B、反比例函数 |
| C、对数函数 | D、指数函数 |
函数y=
-2x的导数是( )
| 2x2+1 |
| x |
A、2-
| ||
B、-
| ||
C、x-
| ||
D、
|
 如图,在四棱锥P-ABCD中,PA=PB=PD=AB=BC=CD=DA=DB=2,E为的PC中点.
如图,在四棱锥P-ABCD中,PA=PB=PD=AB=BC=CD=DA=DB=2,E为的PC中点.