题目内容
18.函数y=-cosx-1的最大值是( )| A. | 1 | B. | 0 | C. | 2 | D. | -1 |
分析 根据余弦函数的有界性,即可求出函数y=-cosx-1的最值.
解答 解:∵-1≤cosx≤1,
∴-1≤-cosx≤1,
∴-2≤-cosx-1≤0;
即函数y=-cosx-1的最大值是0.
故选:B.
点评 本题考查了余弦函数的图象与性质的应用问题,是基础题目.

练习册系列答案
相关题目
8.已知函数f(x)是定义在R上的奇函数,当x≤0时,f(x)=x(1-x),若数列{an}满足a1=$\frac{1}{2}$,且an+1=$\frac{1}{1-{a}_{n}}$,则f(-a2016)( )
| A. | 2 | B. | -2 | C. | 6 | D. | -6 |
10.执行如图所示的程序框图,则输出的结果是( )


| A. | $\frac{19}{20}$ | B. | $\frac{20}{21}$ | C. | $\frac{21}{22}$ | D. | $\frac{22}{23}$ |
8.已知集合A={x|x2-1≤0},B={x|lnx<0},则A∪B=( )
| A. | {x|x≤1} | B. | {x|0<x<1} | C. | {x|-1≤x≤1} | D. | {x|0≤x≤1} |
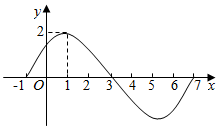 下图为函数y=Asin(ωx+φ)的一段图象,已知A>0,ω>0,φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).
下图为函数y=Asin(ωx+φ)的一段图象,已知A>0,ω>0,φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).