题目内容
17.已知函数f(x)=$\frac{x}{{e}^{x}}$+x2-x(其中e=2.71828…).(Ⅰ)求f(x)在(1,f(1))处的切线方程;
(Ⅱ)若函数g(x)=ln[f(x)-x2+x]-b的两个零点为x1,x2,证明:$\frac{1}{2}$[g′(x1)+g′(x2)]>g′($\frac{{x}_{1}+{x}_{2}}{2}$).
分析 (Ⅰ)求出函数的导数,求得而且像的斜率和切点,运用点斜式方程可得切线的方程;
(Ⅱ)求出g(x)的解析式,求出导数,可得单调区间和极值、最值,可得零点的范围,原不等式可化为$\frac{1}{2}$($\frac{1}{{x}_{1}}$-1+$\frac{1}{{x}_{2}}$-1)>$\frac{2}{{x}_{1}+{x}_{2}}$-1,化简整理,再由基本不等式即可得证.
解答 解:(Ⅰ)函数f(x)=$\frac{x}{{e}^{x}}$+x2-x的导数为f′(x)=$\frac{1-x}{{e}^{x}}$+2x-1,
f(x)在(1,f(1))处的切线斜率为k=f′(1)=1,切点为(1,$\frac{1}{e}$),
可得f(x)在(1,f(1))处的切线方程为y-$\frac{1}{e}$=x-1,
即为y=x-1+$\frac{1}{e}$;
(Ⅱ)证明:函数g(x)=ln[f(x)-x2+x]-b=ln$\frac{x}{{e}^{x}}$-b=lnx-x-b,
g′(x)=$\frac{1}{x}$-1=$\frac{1-x}{x}$,当x>1时,g′(x)<0,g(x)递减;
当0<x<1时,g′(x)>0,g(x)递增.
可得g(x)在x=1处取得极大值,且为最大值-1-b,
设0<x1<1,x2>1,则$\frac{1}{2}$[g′(x1)+g′(x2)]>g′($\frac{{x}_{1}+{x}_{2}}{2}$),
即为$\frac{1}{2}$($\frac{1}{{x}_{1}}$-1+$\frac{1}{{x}_{2}}$-1)>$\frac{2}{{x}_{1}+{x}_{2}}$-1,
即$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$>$\frac{4}{{x}_{1}+{x}_{2}}$,即有(x1+x2)($\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$)>4,
由x1+x2>2$\sqrt{{x}_{1}{x}_{2}}$,$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$>2$\sqrt{\frac{1}{{x}_{1}{x}_{2}}}$,
可得(x1+x2)($\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$)>4,
故原不等式成立.
点评 本题考查导数的运用:求切线的方程和单调区间、极值和最值,考查不等式的证明,注意运用分析法,考查化简整理的运算能力,属于中档题.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案| A. | R<Q<P | B. | Q<R<P | C. | P<Q<R | D. | R<P<Q |
| A. | (-1,2) | B. | [2,3) | C. | (2,3) | D. | (-1,2] |
| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{7}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
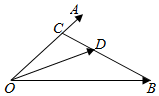 已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,C为线段AO上距A较近的一个三等分点,D为线段CB上距C较近的一个三等分点,则用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{OD}$=$\frac{4}{9}\overrightarrow{a}$$+\frac{1}{3}\overrightarrow{b}$.
已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,C为线段AO上距A较近的一个三等分点,D为线段CB上距C较近的一个三等分点,则用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{OD}$=$\frac{4}{9}\overrightarrow{a}$$+\frac{1}{3}\overrightarrow{b}$.