题目内容
2.如果a+b=1,那么ab的最大值是( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
分析 由于求ab的最大值,只考虑a,b>0时即可.利用基本不等式的性质即可得出.
解答 解:由于求ab的最大值,只考虑a,b>0时即可.
∵a+b=1,∴$1≥2\sqrt{ab}$,解得ab≤$\frac{1}{4}$,当且仅当a=b=$\frac{1}{2}$时取等号.
那么ab的最大值是$\frac{1}{4}$.
故选:B.
点评 本题考查了不等式的基本性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
12.任意a∈R,曲线y=ex(x2+ax+1-2a)在点P(0,1-2a)处的切线l与圆C:x2+2x+y2-12=0的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 以上均有可能 |
13.已知F1,F2分别是双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1(a,b>0)$的两个焦点,过其中一个焦点与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M,若点M在以线段F1F2为直径的圆内,则双曲线离心率的取值范围是( )
| A. | (1,2) | B. | (2,+∞) | C. | $(1,\;\sqrt{2})$ | D. | $(\sqrt{2},\;+∞)$ |
10.某小学共有学生2000人,其中一至六年级的学生人数分别为400,400,400,300,300,200.为做好小学放学后“快乐30分”活动,现采用分层抽样的方法从中抽取容量为200的样本进行调查,那么应抽取一年级学生的人数为( )
| A. | 120 | B. | 40 | C. | 30 | D. | 20 |
17.已知f(x)=log3x,f(a)>f(2),那么a的取值范围是( )
| A. | {a|a>2} | B. | {a|1<a<2} | C. | $\{a|a>\frac{1}{2}\}$ | D. | $\{a|\frac{1}{2}<a<1\}$ |
7.如果关于x的不等式x2<ax+b的解集是{x|1<x<3},那么ba等于( )
| A. | -81 | B. | 81 | C. | -64 | D. | 64 |
12.已知a=$\sqrt{0.4}$,b=20.4,c=0.40.2,则a,b,c三者的大小关系是( )
| A. | b>c>a | B. | b>a>c | C. | a>b>c | D. | c>b>a |
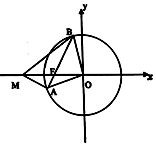 已知圆O:x2+y2=16及圆内一点F(-3,0),过F任作一条弦AB.
已知圆O:x2+y2=16及圆内一点F(-3,0),过F任作一条弦AB.