题目内容
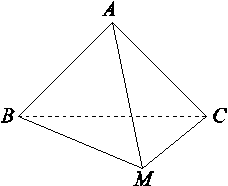
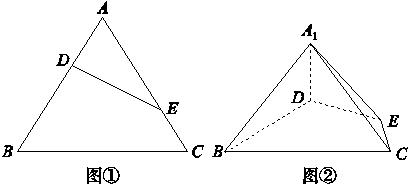
在△ABC中，∠C＝90°，∠B＝30°，AC＝1，M为AB的中点，将△ACM沿CM折起，使A，B间的距离为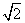
，如图所示，则M到平面ABC的距离为( )
A.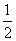
B.
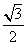C．1 D.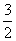
A
[解析] 由题意知MB＝MA＝MC＝1，所以点M在底面的投影为底面三角形的外心，又AB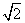＝，AC＝1，BC＝
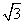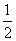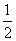，所以底面三角形的外心为斜边BC的中点．设BC的中点为D，连接MD，则MD为M到平面ABC的距离，在△MBD中，∠MBC＝30°，MD⊥BC，所以MD＝MB＝，故选A.
练习册系列答案
长江作业本同步练习册系列答案
相关题目
的值域；
，函数
．若对任意
，总存在
，使
，求实数
的取值范围
表示区域为D，且圆x2＋y2＝4在D内的弧长为
，则实数a的值等于________．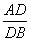
＝
＝
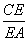是(－∞，＋∞)上的减函数，那么实数a的取值范围是( )
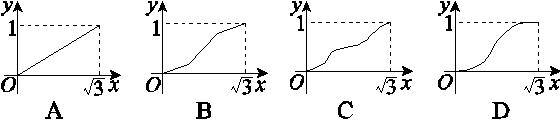
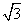)，过点E平行于平面A1BD的截面将正方体分成两部分，其中点A所在的部分的体积为V(x)，则函数y＝V(x)的图象大致为( )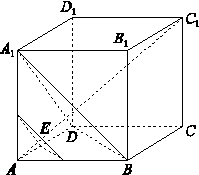
，b＝log2
，c＝log