题目内容
13.函数y=sin$\frac{x}{2}$sin($\frac{π}{2}-\frac{x}{2}$)的最小正周期是( )| A. | 4π | B. | 2π | C. | π | D. | $\frac{π}{2}$ |
分析 根据诱导公式,二倍角的正弦函数公式化简函数解析式,利用三角函数的周期性及其求法运算可得结果.
解答 解:∵y=sin$\frac{x}{2}$sin($\frac{π}{2}-\frac{x}{2}$)=sin$\frac{x}{2}$cos$\frac{x}{2}$=$\frac{1}{2}$sinx,
∴最小正周期T=$\frac{2π}{1}$=2π.
故选:B.
点评 本题主要考查了诱导公式,二倍角的正弦函数公式的应用,考查了三角函数的周期性及求法,属于基础题.

练习册系列答案
相关题目
3.已知复数$z=\frac{2-i}{i^3}$(其中i是虚数单位,满足i2=-1),则z的共轭复数是( )
| A. | 1-2i | B. | 1+2i | C. | -1-2i | D. | -1+2i |
1.在(x+$\frac{1}{x}$)4(2x-1)6的展开式中,常数项为( )
| A. | 6 | B. | 240 | C. | 480 | D. | 486 |
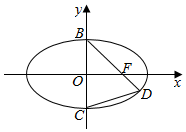 如图,在平面直角坐标系xOy中,F为椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,B,C分别为椭圆的上、下顶点,直线BF与椭圆的另一个交点为D,且直线CD的斜率为$\frac{1}{2}$,则该椭圆的离心率为$\frac{\sqrt{2}}{2}$.
如图,在平面直角坐标系xOy中,F为椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,B,C分别为椭圆的上、下顶点,直线BF与椭圆的另一个交点为D,且直线CD的斜率为$\frac{1}{2}$,则该椭圆的离心率为$\frac{\sqrt{2}}{2}$.