题目内容
. f(x)=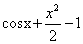
(Ⅰ)求证: 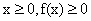 ;
;
(Ⅱ)若不等式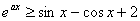 对任意的
对任意的 恒成立,求实数
恒成立,求实数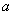 的取值范围.
的取值范围.
(Ⅰ)证明: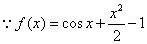
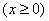 ,则
,则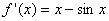 ,设
,设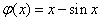 ,则
,则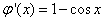 , ………………………2分
, ………………………2分
当 时,
时,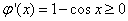 ,即
,即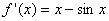 为增函数,所以
为增函数,所以 ,
,
即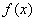 在
在 时为增函数,所以
时为增函数,所以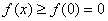 ………………………4分
………………………4分
(Ⅱ)解法一:由(Ⅰ)知 时,
时,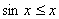 ,
,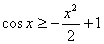 ,所以
,所以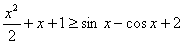 , ………………………6分
, ………………………6分
设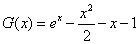 ,则
,则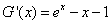 ,设
,设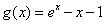 ,则
,则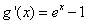 ,
,
当 时
时 ,所以
,所以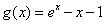 为增函数,所以
为增函数,所以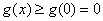 ,所以
,所以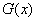 为增函数,所以
为增函数,所以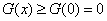 ,所以
,所以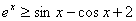 对任意的
对任意的 恒成立. ………………………8分
恒成立. ………………………8分
又 ,
,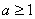 时,
时,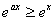 ,所以
,所以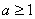 时
时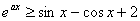 对任意的
对任意的 恒成立. ………………………9分
恒成立. ………………………9分
当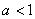 时,设
时,设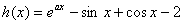 ,则
,则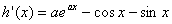 ,
,
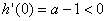 ,所以存在实数
,所以存在实数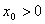 ,使得任意
,使得任意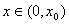 ,均有
,均有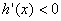 ,所以
,所以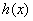 在
在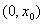 为减函数,所以在
为减函数,所以在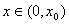 时
时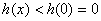 ,所以
,所以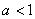 时不符合题意.
时不符合题意.
综上,实数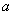 的取值范围为
的取值范围为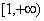 . …………………………12分
. …………………………12分
(Ⅱ)解法二:因为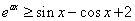 等价于
等价于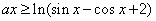 …………6分
…………6分
设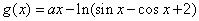 ,
,
则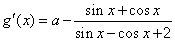
可求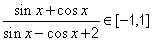 , ……………………………8分
, ……………………………8分
所以当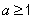 时,
时,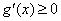 恒成立,
恒成立,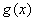 在
在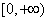 是增函数,
是增函数,
所以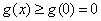 ,即
,即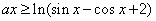 ,即
,即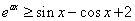
所以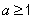 时,
时,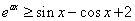 对任意
对任意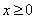 恒成立。……………………………9分
恒成立。……………………………9分
当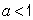 时,一定存在
时,一定存在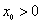 ,满足在
,满足在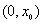 时,
时,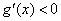 ,所以
,所以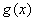 在
在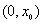 是减函数,
是减函数,
此时一定有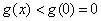 ,即
,即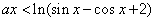 ,即
,即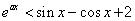 ,不符合题意,故
,不符合题意,故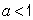 不能满足题意,
不能满足题意,
综上所述,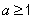 时,
时,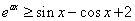 对任意
对任意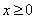 恒成立。……………………12分
恒成立。……………………12分

练习册系列答案
相关题目
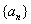 的前
的前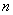 项和为
项和为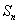 ,点
,点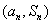 在直线
在直线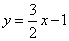 上.
上.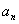 与
与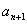 之间插入
之间插入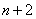 个数组成公差为
个数组成公差为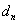 的等差数列,
的等差数列,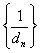 的前
的前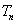 ,并求使
,并求使 成立的正整数
成立的正整数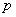 :存在
:存在 ,使关于x的不等式
,使关于x的不等式 成立;命题
成立;命题 :关于x的方程
:关于x的方程 有解;若命题
有解;若命题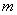 的取值范围.
的取值范围. 图象的一条对称轴方程是
图象的一条对称轴方程是 ,将函数
,将函数 轴向左平移
轴向左平移 得到函数
得到函数
 B.
B. 
 D.
D. 
 的侧棱
的侧棱 上各有一个动点P、
上各有一个动点P、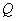 ,且满足
,且满足 ,M是棱CA上的动点,则
,M是棱CA上的动点,则 的最大值是 .
的最大值是 .
 ,如果
,如果
 ,
, ,那么
,那么 等于( )
等于( ) B.
B. 
 D.
D. 
 的导函数为
的导函数为 ,且
,且 >0,
>0, 的图象与x
的图象与x 的最小值为 ( )
的最小值为 ( ) C.2 D.
C.2 D.
 )如图所示,则该几何体的体积等于( )
)如图所示,则该几何体的体积等于( ) B.
B. C.
C. D.
D.

 ,其中常数
,其中常数 .
. 的单调增区间与单调减区间;
的单调增区间与单调减区间; ,求
,求 的取值范围及不超过
的取值范围及不超过 的最大整数
的最大整数 .
.