题目内容
18．已知一个四棱锥的三视图如图所示，则此四棱锥的体积为$\frac{5}{3}$．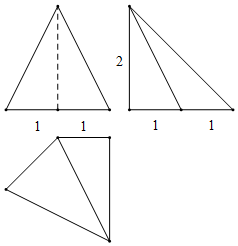
分析 如图所示，该几何体为如下四棱锥：P-ABCD，其中PA⊥底面ABCD，底面四边形由直角梯形ABED，直角△DCE，AB∥DE，AB⊥BC，AB=1，DE=2，BE=EC=1，PA=2．
解答 解：如图所示，该几何体为如下四棱锥：P-ABCD，其中PA⊥底面ABCD，底面四边形由直角梯形ABED，直角△DCE，AB∥DE，AB⊥BC，AB=1，DE=2，BE=EC=1，PA=2．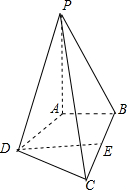
∴S底面ABCD=$\frac{1+2}{2}×1$+$\frac{1}{2}×2×1$=$\frac{5}{2}$．
V=$\frac{1}{3}×\frac{5}{2}×2$=$\frac{5}{3}$．
故答案为：$\frac{5}{3}$．
点评 本题考查了四棱锥的三视图、体积的计算公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
8．已知a，b，c，d都是常数，a＞b，c＞d，若f（x）=2017-（x-a）（x-b）的零点为c，d，则下列不等式正确的是（ ）
| A． | a＞c＞b＞d | B． | a＞b＞c＞d | C． | c＞d＞a＞b | D． | c＞a＞b＞d |
9．已知集合A={x∈R||x|＜2}，B={x∈R|x+1≥0}，则A∩B=（ ）
| A． | （-2，1] | B． | [-1，2） | C． | [-1，+∞） | D． | （-2，+∞） |
6．已知定义在R上的函数f（x）=sinωx（ω＞0）的图象与x轴的两个相邻交点的距离等于$\frac{π}{2}$，若将函数y=f（x）的图象向左平移$\frac{π}{6}$个单位得到函数y=g（x）的图象，则使y=g（x）是减函数的区间为（ ）
| A． | $（{\frac{π}{4}，\frac{π}{3}}）$ | B． | $（{-\frac{π}{4}，\frac{π}{4}}）$ | C． | $（{0，\frac{π}{3}}）$ | D． | $（{-\frac{π}{3}，0}）$ |
13．已知函数y=5cos（$\frac{2k+1}{3}$πx-$\frac{π}{6}$）（其中k∈N），对任意实数a，在区间[a，a+3]上要使函数值$\frac{5}{4}$出现的次数不少于4次且不多于8次，则k值为（ ）
| A． | 2或3 | B． | 4或3 | C． | 5或3 | D． | 8或3 |
5．设函数f（x）=$\left\{\begin{array}{l}{（\frac{1}{3}）^{-x}-2，x≥0}\\{2lo{g}_{3}（-x），x＜0}\end{array}\right.$若f（m）＞1，则m的取值范围是（ ）
| A． | （1，+∞） | B． | （-$\sqrt{3}$，1） | C． | （-∞，-$\sqrt{3}$）∪（1，+∞） | D． | （-∞，-$\sqrt{3}$） |
12．若直线l∥平面α，直线a?α，则l与α的位置关系是（ ）
| A． | l∥α | B． | l与α异面 | C． | l与α相交 | D． | l与α没有公共点 |