题目内容

8．命题p：?x∈N，x2≥x，则该命题的否定是?x∈N，x2＜x．

分析 根据特称命题的否定是全称命题进行求解即可．

解答 解：，他是特称命题，则命题的否定是全称命题，
即：?x∈N，x2＜x，
故答案为：?x∈N，x2＜x

点评 本题主要考查含有量词的命题的否定，比较基础．

练习册系列答案
相关题目
18．设f（x）=$\left\{\begin{array}{l}{{x}^{2}（x≤0）}\\{cosx-1（x＞0）}\end{array}\right.$，试求${∫}_{-1}^{\frac{π}{2}}$f（x）dx．
19．若曲线C1：y=x2与曲线C2：y=aex（a＞0）至少存在两个交点，则a的取值范围为（　　）
A．[$\frac{8}{{e}^{2}}$，+∞）B．（0，$\frac{8}{{e}^{2}}$]C．[$\frac{4}{{e}^{2}}$，+∞）D．（0，$\frac{4}{{e}^{2}}$]
16．在等差数列{an}中，a1=-2 012，其前n项和为Sn，若$\frac{{{S_{12}}}}{12}-\frac{{{S_{10}}}}{10}$=2，则S2012的值等于（　　）
A．-2 011B．-2 012C．-2 010D．-2 013
3．若i是虚数单位，
（1）已知复数Z=$\frac{5{m}^{2}}{1-2i}$-（1+5i）m-3（2+i）是纯虚数，求实数m的值．
（2）如不等式m2-（m2-3m）i＜（m2-4m+3）i+10成立，求实数m的值．
13．已知函数y=f（n），满足f（0）=3，且f （n）=nf（n-1），n∈N+，则f（3）=（　　）
A．6B．9C．18D．24
20．已知二次函数f（x）满足f（x+1）-f（x）=2x，且f（0）=1．
（1）求f（x）的解析式；
（2）若函数y=f（x+m）在[-1，1]上单调，求m的取值范围；
（3）当x∈[-1，1]时，不等式f（x）＞2x+m恒成立，求实数m的范围．
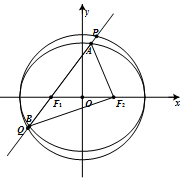17．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）和圆O：x2+y2=a2，F1（-1，0），F2（1，0）分别是椭圆的左、右两焦点，过F1且倾斜角为α$（{α∈（{0，\frac{π}{2}}]}）$的动直线l交椭圆C于A，B两点，交圆O于P，Q两点（如图所示，点A在x轴上方）．当α=$\frac{π}{4}$时，弦PQ的长为$\sqrt{14}$． 
（1）求圆O与椭圆C的方程；
（2）若2|BF2|=|AF2|+|AB|，求直线PQ的方程．
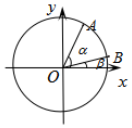18．如图，在平面直角坐标系xOy中，以x轴为始边作两个锐角α，β，它们的终边分别与单位圆交于A，B两点．已知$A（\frac{{\sqrt{5}}}{5}，\;\frac{{2\sqrt{5}}}{5}）\;，\;\;B（\frac{{7\sqrt{2}}}{10}，\;\frac{{\sqrt{2}}}{10}）$
（1）求tan（α+β）的值；
（2）求2α+β的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网