题目内容
若x,y∈R,A={(x,y)|y=x},B={(x,y)|
=1},则A、B关系为( )
| y |
| x |
| A、A?B | B、A?B |
| C、A=B | D、A⊆B |
考点:集合的相等
专题:集合
分析:A={(x,y)|y=x},由于x∈R,可知:A的点(x,y)为直线y=x上的所有点.B={(x,y)|
=1},可知:x≠0,因此:B的点(x,y)为直线y=x上去掉(0,0)后剩下的所有点.即可得出.
| y |
| x |
解答:
解:A={(x,y)|y=x},由于x∈R,可知:A的点(x,y)为直线y=x上的所有点.
B={(x,y)|
=1},可知:x≠0,因此:B的点(x,y)为直线y=x上去掉(0,0)后剩下的所有点.
∴B?A.
故选:B.
B={(x,y)|
| y |
| x |
∴B?A.
故选:B.
点评:本题考查了集合之间的关系、函数的定义域,属于基础题.

练习册系列答案
相关题目
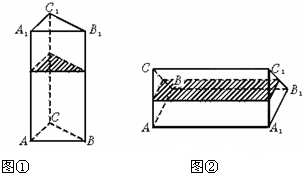 如图①是一个正三棱柱形容器,底面边长为a,高为2a,内装水若干.将容器放倒,把一个侧面作为底面,如图②,这时水面恰好为中截面.请问图①中容器内水面的高度是多少?
如图①是一个正三棱柱形容器,底面边长为a,高为2a,内装水若干.将容器放倒,把一个侧面作为底面,如图②,这时水面恰好为中截面.请问图①中容器内水面的高度是多少?